Heat. Calorie, British thermal unit. Heat capacity. Specific heat. Method of mixtures. Changes of phase. Heat of fusion, vaporization. Sublimation. Evaporation. Liquefaction of gases. Critical temperature and pressure. PVT surface.

Units of heat. The three units most commonly used in measuring quantity of heat are calorie, kilocalorie, and British thermal unit defined as follows:

Calorie. The amount of heat needed to raise the temperature of one gram of water one Centigrade degree.

Kilocalorie. The amount of heat needed to raise the temperature of one kilogram of water one Centigrade degree.

British thermal unit. The amount of heat needed to raise the temperature of one pound of water one Fahrenheit degree.

Substance	Specific Heat
Water	1.00
Alcohol	0.65
Aluminum	0.22
Glass	0.20
Iron	0.11
Copper, Brass	0.09
Silver	0.06
Lead	0.03

Table 1

Specific heat. The number of calories needed to raise the temperature of one gram of a substance one Centigrade degree; or the number of British thermal units needed to raise the temperature of one pound of a substance one Fahrenheit degree. See Table 1.

Example. The specific heat of iron is 0.107 cal/g C^o. It is also 0.107 Btu/lb F^o.

In general, the specific heat of a substance varies with temperature. However, at ordinary temperatures, and over temperature intervals that are not too great, specific heats can be regarded as constant.

Heat capacity. The amount of heat needed to raise the temperature of a body one degree. It is measured in calories per degree centigrade (cal/C^o) and in Btu per degree Fahrenheit (Btu/F^o)

Note. The specific heat of a substance is the heat capacity of a unit mass of the substance. The specific heat of iron is the heat capacity of one gram of iron.

Phases of matter. In general, matter exists either as a solid, liquid or gas. These three states in which it may exist are called its phases. Provided they don’t decompose at high temperatures, all substances can exist in any of these three phases under the proper conditions of temperature and pressure. Water, for example, exists in the solid phase as ice, in the liquid phase as water, and in the gaseous phase as steam. Transitions from one phase to another are accompanied by the absorption or liberation of heat and usually by a change in volume.

Amount of heat Q gained (or lost) by a body in which there is no change of state. The amount of heat Q gained (or lost) by a body in which there is no change of state is given by

The Method of Mixtures. When two substances of unequal temperatures are brought into contact or mixed, the warmer one will lose heat and the cooler one will gain heat until both finally reach the same temperature. No heat energy is lost when substances of unequal temperatures are mixed. The heat lost by the hot substances will be equal to the heat received by the cooler substances. The number of calories lost by the warmer substances will be equal to the number of calories gained by the cooler substances. The formula that gives the calories (or Btu’s) gained or lost by a substance is

Problem 1. 100g of iron at 80^o C are added to 107g of water at 25^o C. What is the final temperature of the mixture?

Solution. Denote the final temperature by x. The specific heat of iron is 0.107. The number of calories lost by the iron is

Since the number of calories lost by the iron is equal to the number of calories gained by the water we have

Problem 2. A brass cylinder weighing 201.9 g has been heated to a temperature of 100^o C by suspending it in steam. It is put in a calorimeter containing 405 g of water at a temperature of 20^o C. The calorimeter has a mass of 110 g and a specific heat of 0.09 cal/g C^o. The final temperature of the water is 23.5^o. What is the specific heat of the brass cylinder?

Since the heat lost by the brass cylinder is equal to the heat gained by the water and calorimeter, we have

The above method is a general one. In all problems involving heat exchange you identify the substances that lose heat and those that gain heat and remember that the heat lost by the warmer bodies is equal to the heat gained by the cooler bodies.

Fusion is the scientific term for what is commonly called melting. The temperature at which fusion occurs is called the melting point. Pure substances generally have a definite melting point. Different solids have different melting points. Non-crystalline substances like glass and paraffin have no definite melting point. When heated they soften and can then be bent, molded, or welded.

For crystalline substances the melting point and freezing point are the same temperature.

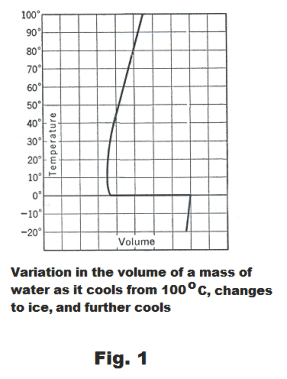
Volume changes during solidification. Most substances contract when they solidify. There are a few exceptions to this rule, however. Water is the most important one. Water expands to a volume of about 1.1 times its original volume when it freezes. Bismuth and antimony are two metals that expand when they solidify.

Volume change in water upon cooling. In Fig. 1 is a graph showing the change in volume of a mass of water as it cools from 100^o C, changes to ice, and cools further. It contracts until it reaches a temperature of 4^o C, then expands slightly as it cools to its freezing point, 0^o C, where it then expands greatly in changing to ice. On further cooling below 0^o, the ice contracts.

It is fortunate that water expands on freezing. If it contracted, the water in a lake would sink to

Effect of pressure on the freezing point of substances. An increase in pressure raises the freezing point of most substances. In substances such as water which expand on freezing, however, an increase in pressure lowers the freezing point.

Heat of fusion of a solid. The amount of heat required to melt 1 unit mass of the solid without changing its temperature.

Heat of vaporization of a liquid. The amount of heat required to vaporize 1 unit mass of the liquid without changing its temperature.

Heat of solidification of a liquid. The amount of heat given up in solidifying 1 unit mass of the liquid without changing its temperature.

Heat of condensation of a gas. The amount of heat given up in condensing 1 unit mass of the gas without changing its temperature.

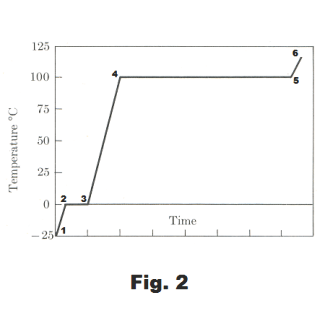
Changes of phase. Consider the following experiment: We take ice from a freezer where the temperature was -25^o C, crush it quickly, place it in a container, and insert a thermometer in it. Imagine that the container is surrounded by a heating coil that supplies heat at a uniform rate and suppose no other heat reaches the ice. The temperature of the ice will be observed to increase steadily until it reaches 0^o C as shown in the graph of Fig. 2 (segment from point 1 to 2). As soon as the temperature has reached 0^o, some liquid water will start appearing in the container. The ice is now melting. The thermometer will show no increase in temperature, even though heat is still being supplied at the same rate as before, until all the ice is melted. (The ice and water must be kept thoroughly mixed, otherwise the part of the water closest to the heater will rise above 0^o.). Once all the ice has melted (point 3 on the graph), the temperature will rise again at a uniform rate until it reaches 100^o (point 4 on the graph). When this point is reached, bubbles of steam (gaseous water, water vapor) start to escape from the liquid surface. The water is now boiling. The temperature will remain constant, even though heat is still being continually supplied, until all the water has boiled away (point 4 to point 5 on the graph). If the water vapor had been trapped instead of being allowed to boil away, the heating process could be continued from point 5 to point 6. The gas would then be called “superheated steam”.

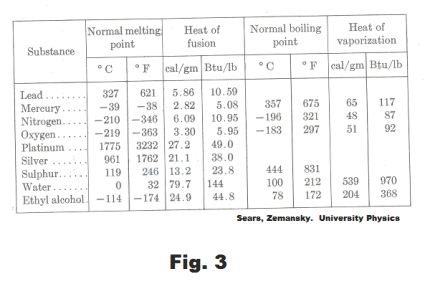
Between points 2 and 3, the ice is going through a change of phase from ice to water. In going through this change of phase the ice absorbs 79.7 calories (its heat of fusion) for each gram of ice. Between points 4 and 5, the water is going through a change of phase from water to steam. In going through this change of phase the water absorbs 539 calories (its heat of vaporization) for each gram of water. See Fig. 3.

We can now reverse the process. We can go from point 6 on the graph back to point 1, by removing heat. At point 5 the steam starts doing a change of phase, condensing, turning back to water. In doing this it gives up 539 calories (its heat of condensation) for each gram of gas. (We note that the heat of condensation is equal to the heat of vaporization.) When it reaches point 4 all the steam has been condensed into water. We continue removing heat until it reaches point 3. At point 3 it starts going through another change of phase, turning from water into ice. In doing this it gives up 79.7 calories (its heat of solidification) for each gram of water. Thus its heat of solidification is equal to its heat of fusion. When all water has been changed to ice we are at point 2. We can then continue removing heat until we get to point 1.

When a substance is going through a change of phase, two phases of the substance are together concurrently. Thus when water is going through a change of phase from water to ice, both water and ice are together concurrently as a mixture in equilibrium. The same is true when water changes to steam.

The above example used water but many substances follow the same type curve shown in Fig. 2. Some substances decompose before reaching a melting or boiling point. Others, such as glass or pitch, do not change state at a definite temperature but become gradually softer as their temperature is raised. Crystalline substances, such as ice or a metal, melt at definite temperatures.

Normal melting point. The temperature at which a crystalline solid melts when heat is supplied to it at atmospheric pressure.

Normal boiling point. The temperature at which a crystalline solid boils when heat is supplied to it at atmospheric pressure.

Under the proper conditions of temperature and pressure, a substance can pass from the solid state to the gaseous state without passing through the liquid state. Camphor, iodine, naphthalene, and dry ice are some examples of substances which will evaporate at atmospheric pressure. Ice and snow are other examples.

Heat of sublimation. The amount of heat required to change 1 unit mass of a substance from solid to vapor at a given temperature.

Evaporation. Evaporation occurs when the surface molecules of a liquid leave the surface and dart off to become gas molecules.

1. Change in temperature. The rate of evaporation increases with an increase in temperature.

2. Size of surface area of the liquid. The larger the surface area of the liquid, the faster the liquid evaporates.

3. The nature of the liquid. Alcohol evaporates more rapidly than water. Some liquids such as olive oil don’t seem to evaporate at all.

4. The air pressure above the liquid. Evaporation becomes more rapid when the atmospheric pressure is reduced.

5. The amount of water vapor in the air above the liquid. The rate of evaporation is decreased when the amount of water vapor in the air above the liquid is increased.

6. Air movement above the liquid. The rate of evaporation increases with increased air movement over the liquid surface.

Liquefaction of gases. Michael Faraday (1791 - 1867) conducted an important series of

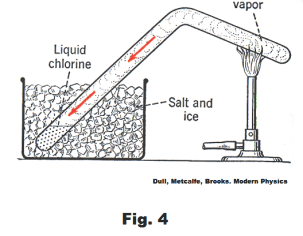
experiments on liquefying gases. In one experiment he filled a tube with chlorine gas using a thick-walled tube of the type shown in Fig. 4. He put one end of the tube in a freezing mixture of salt and ice and heated the other end. The gas in the heated end expanded and increased the pressure on the gas in the cold end and the combined effect of the pressure and the cooling liquified the chlorine. He used the same method to liquefy other gases, including ammonia and carbon dioxide, but was unable to liquefy oxygen, hydrogen and nitrogen in this way. We now know why he was unable to liquefy oxygen, hydrogen and nitrogen by this method. His freezing mixture was not cold enough to liquefy them no matter how much pressure is exerted on them. Oxygen must be cooled to -119^o C, nitrogen to -147^o C, and hydrogen to -240^o C before they will liquefy at any pressure.

Def. Critical temperature. The temperature to which a gas must be cooled before it will liquefy.

Def. Critical pressure. The pressure needed to liquefy a gas at its critical temperature.

All known gases have now been liquefied by greatly compressing them, cooling them, and then allowing them to expand, a process that cools them further.

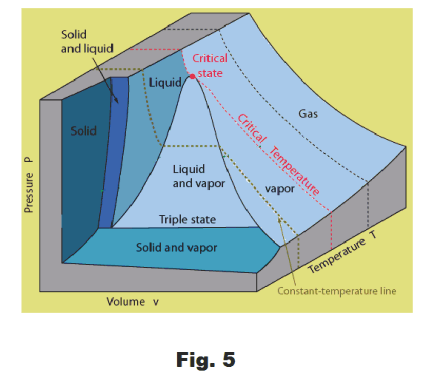
Pressure -Volume -Temperature (PVT) surfaces. Fig. 5 shows the Pressure - Volume - Temperature (PVT) surface of a typical substance. A PVT surface shows the particular phase in which a substance exists (solid, liquid, or gas) for any given set of values of the pressure, volume and temperature (P, V, T) for a unit mass of the substance.

That surface that corresponds to the collection of all possible (P, V, T) triples that can exist for a unit mass of a substance is called its PVT surface. A PVT surface can be viewed as an empirical equation of state of the substance.

The PVT surface thus shows those areas for which a substance exists as a gas, as a liquid, as a solid, etc.