Surface tension

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Surface tension

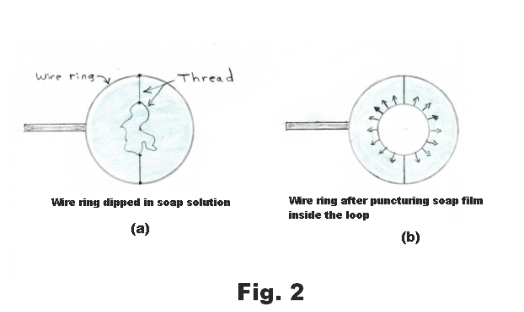
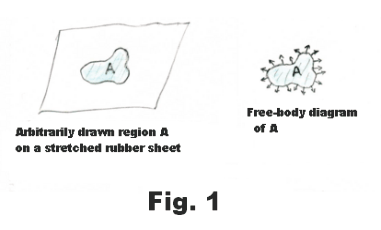
Tensive properties of a liquid surface. Surface tension. There is, on the surface of a liquid, a layer, several molecules deep, that has properties that are different from those of the rest of the liquid. This top layer has tensive properties analogous to those of a stretched elastic sheet. In Fig. 1 is shown a free-body diagram of an arbitrarily drawn region A on a rubber sheet. On the free-body diagram there are outwardly directed tensive forces along the border of the region as shown in the figure. If we were to delineate some arbitrary region on the surface of a liquid and draw the free-body diagram of the region, it would look the same as that of the rubber sheet shown in Fig. 1. An experiment that illustrates this fact is the following: Construct a wire ring several inches in diameter and attach threads to it creating a loose loop of thread as shown in Fig. 2 (a). Now dip the ring into a soap solution. A thin soap film will be formed inside the ring where the threads will float freely. Now puncture the soap film inside the loop with a hot wire. On puncturing, the loop of thread will spring out into the circle shown in Fig. 2 (b). The surfaces of the liquid pull radially out on the thread, pulling it out into a circle, due to their elastic character. The same forces that pulled it out were acting before the film was punctured but they were counterbalanced by forces from the film inside the thread.

There are many phenomena that illustrate the elastic properties of the surface of a liquid. If you lay a sewing needle or razor blade or paper clip carefully on the surface of water they will make a small indentation in the surface and float, as though they were lying on an elastic sheet, even though their density may be up to ten times that of water. When a liquid is squeezed from a medicine dropper it comes out, not as a continuous stream, but as drops, due to the tensive surface forces that tend to pull it into the form of a sphere.

We refer to the contractive, tensive force in the surface layer of a liquid as surface tension. We now consider ways of measuring the surface tension of a liquid.

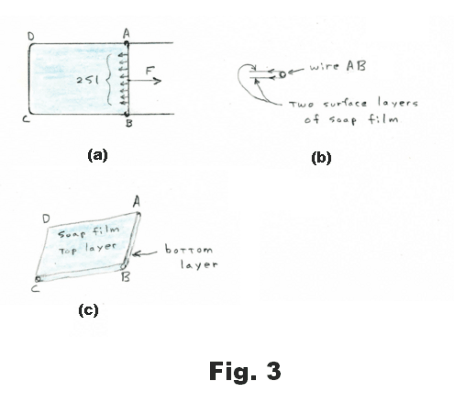
Measurement of surface tension. Construct a rectangular wire frame with one side movable as shown in Fig. 3 (a). Side AB is a second piece of wire that serves as a slider, moving easily along the two legs of the frame. If we dip this frame into a soap solution the tensive forces of the soap film quickly pull the slider AB to the far left end. If we exert a force F to pull the slider to the right, the force F will be opposed by the tensive pull of the soap film. As we pull the slider AB to the right, the force F required to pull it remains constant. The same force F will hold the slider at rest in any position, regardless of the area of the liquid film, provided the film remains at constant temperature. This represents an important difference between the elastic behavior of the surface of a liquid and the elastic behavior of a sheet of rubber. If we stretch a sheet of rubber, the force F required to stretch it increases as we stretch.

We now make an observation in regard to soap film. Although soap film is very thin, its thickness is enormous in comparison with the size of a molecule. Soap film has a top tensive layer and a bottom tensive layer, each several molecules thick. Sandwiched between the two surface layers is the main part of the film consisting of bulk liquid. See Fig. 3 (c).

As the slider AB is pulled to the right and the area of the film is increased, molecules from the main body of the film move into the surface layers. Thus the surface areas are not “stretched” as a rubber sheet would be but more surface is created from the bulk liquid.

Let the length of the wire slider AB be l. Since the film has two surfaces (top and bottom), the total length over which the tensive forces of the film act is 2l. See Fig. 3 (b). The surface tension S is defined as the force exerted by a single surface on a section of unit length. Thus the total tensive force pulling to the left on the slider in Fig. 3(a) is 2Sl. Consequently, F = 2Sl and we have the formula

which can be used for computing the surface tension S of a soap film. Surface tension is expressed in dynes/cm in the cgs system.

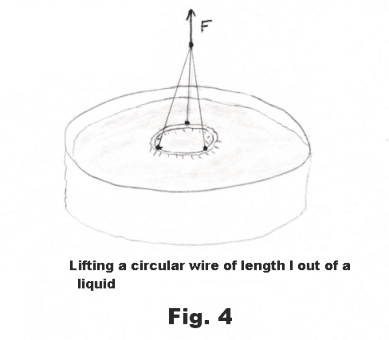
One of the methods commonly used to measure the surface tension of liquids is to measure the force required to lift a circular wire of length l out the body of a liquid. See Fig. 4. The force F required to lift it, minus the weight w of the wire, represents the force, that is needed to balance the surface tensile forces 2Sl, from the two surface films on each side of the wire. The force can be measured by the stretch of a delicate spring or by the twist of a torsion wire. The surface tension is then given by

S = (F - w)/2l

Surface tension viewed as work done per unit area in increasing the area of a film. There is another way in which to view surface tension. Let us go back and consider Fig. 3 in which we pull the slider to the right with a force F. The work done in moving the slider AB through a distance x is

W = Fx

and since

F = 2Sl

the work done is given by

W = S×2lx

Now 2lx is the increase in surface area of the film. Setting 2lx = ΔA we have

Thus surface tension can be viewed as the work done per unit area in increasing the area of a film.

Pressure inside a soap bubble. The formula for the pressure inside a soap bubble is

where

p = pressure inside the soap bubble

p_a = atmospheric pressure

S = surface tension of soap solution

R = radius of soap bubble

_________________________________________________________________

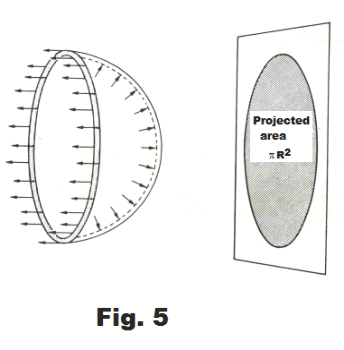
Derivation. In Fig. 5 is shown a free-body diagram of half of a soap bubble. A soap bubble consists of two concentric spherical surfaces, its inner and outer tensive surfaces, with bulk liquid between. Applying the principles of statics to the free-body diagram, we must have for static equilibrium

Σ F_x = 0

i.e. the sum of the forces in the x direction must equal zero. Thus the sum of the forces in the positive x direction must be equal to the sum of the forces in the negative x direction. The sum of the forces to the left (-x direction) coming from the inner and outer surfaces is given by

3) Σ F (-x direction) = 2×S×2πR = 4πRS

We wish now to find an expression for the sum of the forces in the +x direction. These correspond to the x components of the outward pointing forces on the right half-sphere of the bubble shown in Fig. 5.

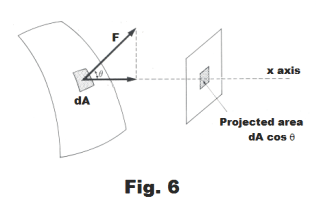
Due to the air pressure within the soap bubble, there is, corresponding to every point P on the soap bubble, a force F normal to the surface which is given by

F = (p - p_a)dA

where p is the pressure inside the soap bubble, p_a is the pressure of the atmosphere, and dA is an infinitesimal element of area at point P.

The x component of this force is given by

F_x = F cos θ = (p - p_a)dA cos θ

where θ is the angle between F and the positive x axis. See Fig. 6.

Let Q represent the outer surface of the right half-sphere. See Fig. 7. Then the sum of the forces in the positive x direction is given by

4) Σ F ( +x direction) = ∫_Q (p - p_a)dA cos θ = (p - p_a) ∫_Q dA cos θ.

We now observe that the product dA cos θ corresponds to the projection of the infinitesimal area dA on a plane perpendicular to the X axis as shown in Fig. 6. Thus

∫_Q dA cos θ = πR²

See Fig. 5. Hence 4) becomes

5) Σ F ( +x direction) = (p - p_a) πR²

From 3) and 5) we get

(p - p_a) πR² = 4πRS

_________________________________________________________________

Pressure inside a spherical drop of liquid. The pressure inside a spherical drop of liquid is given by the formula

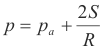
Derivation. The derivation is essentially the same as for a soap bubble. In the case of a drop there is only a single tensive surface.

References

Sears, Zemansky. University Physics.

Semat, Katz. Physics.

Dull, Metcalfe, Brooks. Modern Physics.