Streamline flow. Equation of continuity. Bernoulli�s Theorem. Venturi tube. Torricelli�s theorem. Viscosity. Reynolds number.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Streamline flow. Equation of continuity. Bernoulli’s Theorem. Venturi tube. Torricelli’s theorem. Viscosity. Reynolds number.

Streamline flow. The motion of fluids can be very complex and difficult to analyze. The turbulent flow of a mountain stream or the complicated air movements of the atmosphere are examples of this. However, there is an important type of fluid flow that is relatively simple. It is the smooth, steady, non-turbulent flow of a fluid through a tube called streamline flow or laminar flow. See Fig. 1. The flow of fluid in a tube is of the streamline type if the velocity is not too great and there are not bends or changes in diameter so abrupt as to cause turbulence. With streamline flow the path of any particle of fluid as it moves through the tube is called a streamline. One can map the flow of fluid through a tube by drawing a number of streamlines following the paths of the particles of the liquid. The rate of flow can be represented by the density of the streamlines. In streamline flow the velocity of the fluid at any chosen point within the tube is always the same.

Rate of flow of a fluid in a pipe. The rate of flow of a fluid in a pipe is given by

R = Av

where A is the cross section area and v is the velocity of the fluid.

Example. A fluid is flowing at a velocity of 5 ft/sec in a pipe with a cross section area of 2 ft². Its rate of flow is then 10 ft³/sec.

The equation of continuity. In steady state flow of an incompressible fluid through a tube of varying cross section area

A₁v₁ = A₂v₂

where v₁, v₂ are respectively the velocities of the fluid at cross sections A₁, A₂.

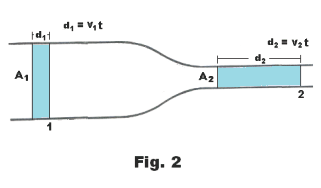
Derivation. Consider the fluid flow shown in Fig. 2 where the cross-section area at point 1 is A₁ and at point 2 is A₂. In time t, the fluid at point 1 will advance a distance of d₁ = v₁t and a volume of liquid equal to A₁d₁ = A₁v₁t will pass point 1. Similarly, the volume of fluid passing point 2 in time t will be A₂v₂t. The volume of fluid passing points 1 and 2 in time t must be equal so

A₁v₁t = A₂v₂t

and

A₁v₁ = A₂v₂

which is the equation of continuity for the steady flow of an incompressible liquid.

Bernoulli’s Theorem. Bernoulli’s theorem states a relationship between pressure, velocity and elevation at points along a flowing stream of fluid . Given: steady, streamline flow of an incompressible, nonviscous fluid in a tube of varying diameter. Then for any two points along the flow

p + ρgh + ½ ρv² = constant

where ρ is the density of the fluid and p, v and h are the pressure, velocity and height (i.e. elevation) at any chosen point in the stream.

In words, the theorem states that at any two points along the stream the sum of the pressure (p), the potential energy of a unit volume of the fluid (ρgh) and the kinetic energy of a unit volume of the fluid (½ ρv² ) has the same value.

Bernoulli’s equation assumes streamline frictionless flow. If the tube is smooth, large in diameter, short in length and if the fluid has a small viscosity and flows slowly, the frictional resistance may be small enough to neglect.

______________________________________________________

Proof. Fig. 3 represents a section of a tube in which an incompressible, nonviscous fluid is flowing with streamline flow. The wide part of the tube has a cross section area A₁ and the narrow part has a cross section area A₂. At all points in the wide part the pressure is p₁ and the velocity is v₁. At all points in the narrow part the pressure is p₂ and the velocity is v₂.

As the fluid (shown in color) is being pushed to the right by a force equal to p₁A₁through a distance d_1, work is done on the system.

Work done on the system = p₁A₁d₁

At the same time, the right end advances a distance d₂ against an external force p₂A₂ acting in the opposite direction. Work is thus done by the system.

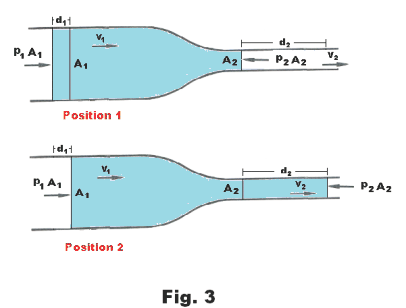
Work done by the system = p₂A₂d₂

To move the system from Position 1 to Position 2, a net amount of work must be done by some agent (a pump, in this case) equal to

1) Net work done on the system = p₁A₁d₁ - p₂A₂d₂

Now the volumes A₁d₁ and A₂d₂ must be equal. Denote their volumes by V i.e.

V = p₁A₁ = p₂A₂

The mass m of the fluid in sections A₁d₁ and A₂d₂ is given by ρV where ρ is the density of the fluid. Thus

p₁A₁ = p₂A₂ = m/ρ

Consequently, from 1),

There is a net change in kinetic energy that occurs. It is given by

Net change in kinetic energy = ½ mv₂² - ½ mv₁²

In the figure, the tube is horizontal and there is no change in gravitational potential energy. However, in the general case, the section A₂d₂ on the right side may be at a different elevation than the section A₁d₁ on the left side and the net change in gravitational potential energy is given by

Net change in gravitational potential energy = mgh₂ - mgh₁

where h₂ and h₁ are the respective elevations of the sections A₂d₂ and A₁d₁ above some arbitrary reference point.

The net work done on the system is equal to the sum of the increases in the kinetic energy and the gravitational potential energy. Thus

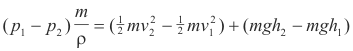
Multiplying by ρ/m we obtain

p₁ + ρgh₁ + ½ ρv₁² = p₂ + ρgh₂ + ½ ρv₂²

p + ρgh + ½ ρv² = constant

______________________________________________________

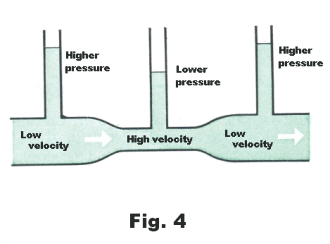
The Venturi tube. A Venturi tube consists of a tube with a narrow, constricted area as shown in Fig. 4. Because the fluid flows more rapidly through the constricted part of the tube, the pressure there is less, in accordance with Bernoulli’s theorem. This idea find application in many devices.

Torricelli’s theorem. The velocity v of outflow of a liquid from an orifice in a tank is

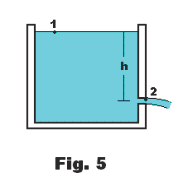
where h is the depth of the orifice below the surface of the liquid as shown in Fig. 5.

Note that the velocity of outflow is the same as that which would be acquired by a body freely falling from rest through a distance h.

_______________________________

Derivation. We apply Bernoulli’s equation to points 1 at the surface and 2 at the orifice as shown in the figure. We choose as reference level for the measurement of potential energy the height of the orifice. The pressure at both points 1 and 2 is the atmospheric pressure p_atm since both are open to the atmosphere. If the orifice is small, the level of the liquid in the tank will fall very slowly and we will assume it to be zero i.e. v₁ = 0. Bernoulli’s equation then becomes

p_atm + ρgh + 0 = p_atm + 0 + ½ ρv²

_______________________________

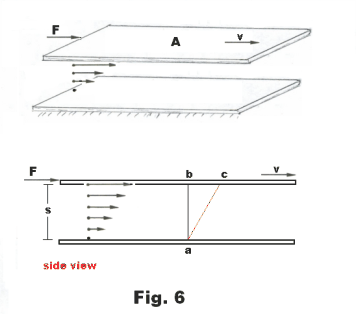
Laminar flow of liquids and viscosity. In the laminar flow of liquids the liquid can be conceived of as consisting of thin lamina or sheets that slide over each other in a similar way to the way in which the leaves of a book will slide over each other if we lay the book on a table and apply a horizontal force to the top cover. In Fig. 6 are two plates with liquid between them. The bottom plate is fixed and the top plate is moving to the right with a velocity v. The layer of liquid next to the top plate will move to the right with a velocity v, the same velocity as the plate. The layer of liquid next to the bottom plate will be at rest. The velocities of the intermediate layers will increase uniformly from the bottom plate to the top as shown in the figure. The cross section ab of liquid (shown in the bottom view) will, a moment later, assume the position ac.

It has been found experimentally that the force F required to keep the moving plate moving at a constant velocity v is directly proportional to the velocity v, inversely proportional to the separation s of the plates, and directly proportional to the area A of the moving plate i.e.

where η is the coefficient of viscosity.

The coefficient of viscosity, or simply viscosity, is small for liquids that flow readily, as water,

and large for highly viscous liquids such as molasses. It can be viewed as a measure of the amount of internal friction between layers of a fluid. It varies considerably with temperature. In the case of liquids it generally decreases with increasing temperature. In the case of gases it generally increases with increasing temperature.

The unit of viscosity is force times distance divided by area times velocity. In the cgs system a coefficient of viscosity of 1 dyne∙sec/cm² is called a poise. Small viscosities are usually expressed in centipoises (1 cp = 10^-2 poise) or micropoises (1 μp = 10^-6 poise).

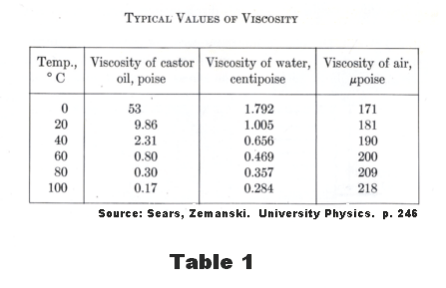
Some typical values of viscosity are given in Table 1.

A common method of measuring viscosity utilizes a small container with a small orifice of specified dimensions in the bottom. A specified amount of liquid is poured in and the time required for the liquid to run out through the orifice is measured. The viscosity is then computed by an empirical formula.

Fluid flow in a pipe. When the velocity of flow is not too large, the flow will be laminar. The laminar flow of a viscous fluid in a pipe will have a velocity profile of the shape shown in Fig. 7. The velocity is a maximum on the axis of the pipe and decreases to zero at the wall. There is a stagnant film of fluid at the wall called the boundary layer.

When the velocity exceeds a certain critical value, the nature of the flow changes and becomes far more complicated. Local circular currents called vortices develop throughout the liquid with a large increase in the resistance to flow. This type of flow is called turbulent flow.

Reynolds number. Reynolds number is a number that is useful in predicting whether flow will be laminar or turbulent. Reynolds number is given by the formula

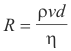
where ρ is the density of the fluid, v is the velocity of flow, η is the viscosity, and d is the diameter of the pipe. Experiments have shown that when the Reynolds number is less than 2000 the flow is always laminar and when it is above 3000 the flow is turbulent. The interval from 2000 to 3000 is a transition region in which the flow is unstable and may change from one type to the other.

References

Schaum. College Physics.

Sears, Zemansky. University Physics.

Semat, Katz. Physics.