Website owner: James Miller
Elasticity. Hook’s Law. Tensile, compressive and shear stresses. Strain. Elastic, shear and bulk modulus.

Def. Elasticity. The ability of a substance to spring back to its original size, shape or volume after being stretched, squeezed, bent etc.
Many materials are elastic to a point. If they are deformed by a force they will return to their original size and shape if the deforming force is within a limit called their elastic limit. Liquids and gases have elasticity of volume. They return to their original volume when the deforming force is released. Liquids and gases have no elastic limit.
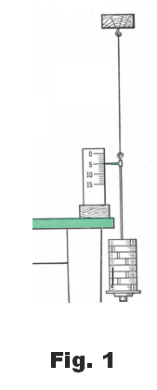
Let us fasten one end of a steel wire to a beam as shown in Fig. 1 and add weights to the hanger attached to its lower end, recording the wire’s length after each weight is added. If we do this we discover that the amount of stretching of the wire is directly proportional to the amount of weight added, provided we don’t pass the wire’s elastic limit. If a weight of 100 g stretches the wire 1 mm, then a weight of 200 g will stretch it 2 mm, a weight of 300 g will stretch it 3 mm, etc. If we remove the weights, the wire will return to its original length. If we continue adding weights in this way we will eventually pass the elastic limit where the wire will not return to its original length when the weights are removed.
Robert Hooke (1635 - 1703) in performing such experiments as the above arrived at Hook’s Law:
Hook’s Law. Within the elastic limit, the amount of distortion in an elastic material is directly proportional to the distorting force.
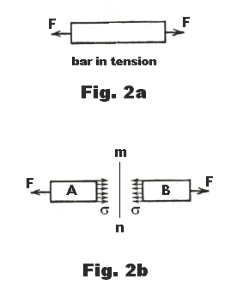
Internal stresses produced by external distorting forces. When external forces act on a body they produce distortion of the body and accompanying internal stresses. Consider a bar of uniform cross-section acted upon by two equal and opposite pulls F at its ends as shown in Fig. 2a. The bar is said to be in tension. Let us now introduce a cutting plane mn that separates the bar into two parts A and B as shown in Fig. 2b. and consider the free-body diagrams of the two parts. Forces F tend to pull the bar apart at cross-section mn and the internal resistive forces σ shown in the figure resist the action and attempt to hold it together. These internal resistive forces σ arise from intermolecular forces that counter the external distorting forces and attempt to return the body to its normal, undistorted size and shape. Since the body is in equilibrium the total of the stress forces σ in part A must be equal to force F and similarly for part B.
A change in size or shape of a body begins when distorting forces are applied to it and stops when the internal resisting stress holds the external forces in equilibrium. If the external forces acting on the body increase to the extent that the maximum stress that can be developed is unable to balance the external forces, the change in form will increase rapidly and the body will break or rupture.
Def. Stress. The internal force that resists change in the size or shape of a body acted on by external forces.
Usage of the term “Stress”. The meaning of the term “stress” depends on context. One may be speaking of the total stress on some section of a body (e.g. total number of pounds of internal resistive force on that section), in which case, his usage should make that clear. The term “stress” is also used extensively to mean “stress per unit area” e.g. pounds per square inch. Thus the term is used in two ways, a possible source of confusion.
Def. Stress or intensity of stress at a point. Stress per unit of area at the point. Its value at any particular point of a section is the stress on an infinitesimally small element of area about the point divided by the area of the element. In general, it varies from point to point in the section. Stresses are expressed in pounds per square foot, tons per square foot, kilograms per square centimeter, etc.
External forces that tend to change the length or shape of a body create resistive internal forces that resist the action.
Def. Tensile stress (or tension). The internal force that resists the action of external forces tending to increase the length (or dimensions) of a body.
Def. Compressive stress (or compression). The internal force that resists the action of external forces tending to decrease the length (or dimensions) of a body.
Three types of stress. At any point in a body there can be any one of the following three types of stress:
1. Tensile stress. Tensile stress is caused by forces that stretch.
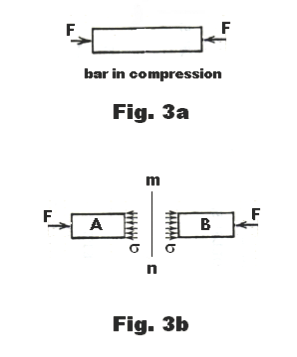
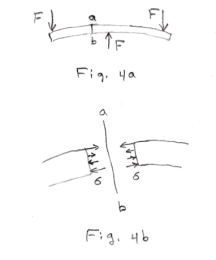
2. Compressive stress. Compressive stress is caused by forces that compress. Fig. 3 shows a bar in compression. Fig. 4 shows a flexed bar. The upper side is in tension and the lower side is in compression.
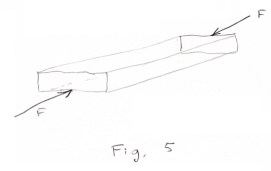
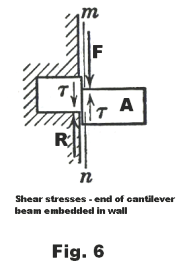
3. Shear stress. See Fig. 5. Here two equal and opposite forces F act on a rectangular block so as to push the top one way and the bottom the other, thus creating shear stress in the block. Shear stresses are forces that resist a tendency for one part of a body to slide over another. In Fig. 6 is depicted the end of a cantilever beam, A, embedded in a wall. Force F represents the weight of the beam and any loads on the beam at the wall. Force R is the reaction of the wall pushing upward. The result of the two opposing forces F and R are the shear stresses τ at the wall.
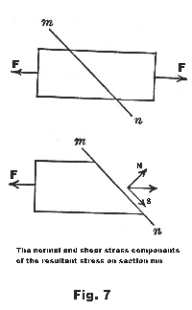
Def. Normal stress. A normal stress on a section is one that acts in a direction perpendicular to the section considered. See Fig. 7.
Def. Unit deformation. Unit deformation is the amount of deformation per unit length of the body. It is determined by dividing the total amount of deformation by the original length of the body (length before the load was applied). If a steel bar 10 inches long is stretched until it is 10.15 inches long the total deformation is 0.15 inches and the unit deformation ε is 0.15 ÷10 = 0.015 inches per inch of original length.
Syn. Strain
The deformations accompanying tension, compression and shear are known, respectively, as elongation, shortening and detrusion.
Def. Strain. The amount of deformation per unit length of the body. The term “strain” is a synonym for “unit deformation”.
Def. Proportionality limit. The highest unit stress at which the stress is proportional to the deformation. It corresponds to that point on a stress-deformation diagram where the curve departs from a straight line.
Def. Elastic limit. The maximum unit stress to which a material may subjected and still be able to return to its original size and shape when the stress is removed.
For many metals there is no appreciable difference between the elastic limit and the proportional limit and the proportional limit is often accepted as the elastic limit.
Def. Modulus of Elasticity (or Young’s modulus). By Hooke’s Law, within the elastic limit of a material, the ratio of the stress to the strain produced in a material is a constant. This constant is called the modulus of elasticity of the material.
![]()
where the stress is given as force per unit area and strain is given as the elongation per unit length. Suppose that a wire or rod of length L and cross section area A experiences an elongation ΔL when a stretching force F is applied to it. Then
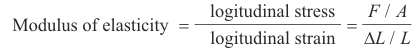
The modulus of elasticity depends only on the material and not on its dimensions. It can be expressed in lb/in2, nt/m2, or dynes/cm2.
For a great many common materials the modulus of elasticity for compression is essentially equal to that for tension and is assumed to be the same for both.
Def. Bulk modulus B. If a body is submerged in water (or other liquid) the increase in pressure on the body due to the weight of the water will cause a decrease in volume. The modulus relating the increase in pressure to the corresponding decrease in volume is called the bulk modulus.
Here the volume stress is equal to the pressure increase Δp and the volume strain is given by
![]()
Thus the bulk modulus B is given by

The reciprocal of the bulk modulus of a material is called the compressibility of the material.
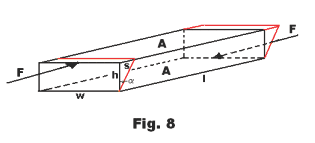
Shear modulus. Consider the rectangular block of height h, width w and length l shown in Fig. 8. A pair of equal and opposite tangential forces F act on the top and bottom shearing the block into a parallelopiped, turning the end faces through the small angle α as shown in red. The area of the top and bottom surfaces is A = w×l.
![]()
![]()
Because the ratio s/h is usually very small, it can be considered as equal to the angle of shear α (expressed in radians). Then
![]()
The shear modulus is sometimes called the modulus of rigidity.
References
Eshbach. Handbook of Engineering Fundamentals.
Schaum. College Physics.
Sears, Zemansky. University Physics.
Semat, Katz. Physics.
Nash. Strength of Materials (Schaum).
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life