Impulse and momentum. Conservation of momentum. Elastic and inelastic collisions. Coefficient of Restitution.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Momentum of a body. The momentum of a body is equal to the mass of the body times its velocity i.e.

1) Momentum = mv

where m is the mass of the body and v is its velocity.

Momentum is a vector quantity whose direction is that of the velocity.

Impulse of a force. The impulse of a force is equal to the force times the length of time the force acts i.e.

2) Impulse = Ft

where F is the force and t is the length of time the force acts.

Impulse is a vector quantity whose direction is that of the force.

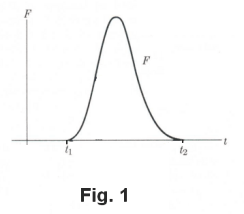
If the force F varies with time (see Fig. 1) the impulse of the force over the time interval [t₁, t₂] is given by

Relationship between impulse and momentum.

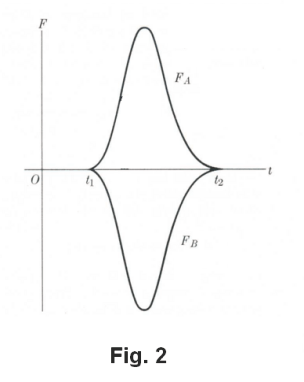
Theorem 1. The change of momentum produced by an impulse is numerically equal to the impulse i.e.

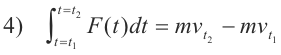
where and are the velocities at times t = t₁ and t = t₂ respectively.

_____________________________________________________

Proof. From Newton’s second law

F = ma

F = m dv/dt

Fdt = m dv

_____________________________________________________

Law of conservation of momentum. In any collision between two or more bodies, the vector sum of the momenta of the bodies after impact is equal to that before impact.

Thus if

m_A, m_B = the masses of bodies A and B

V_A1 , V_B1 = the velocities of bodies A and B before impact

V_A2 , V_B2 = the velocities of bodies A and B after impact

then

the momentum of A plus the momentum of B before the collision

= the momentum of A plus the momentum of B after the collision

5) m_AV_A1 + m_BV_B1 = m_AV_A2 + m_BV_B2

_____________________________________________________

Proof. During a collision of two bodies A and B, body A exerts a force F_A on body B and, by Newton’s Third Law, body B exerts an equal and opposite reactionary force F_B on body A. Fig. 2 shows these two equal and opposite forces over the interval of impact [t₁, t₂]. As a consequence, the impulses of these two forces are equal in magnitude but opposite in sign i.e.

Impulse of F_B = - Impulse of F_A

Thus

m_BV_B2 - m_BV_B1 = -(m_AV_A2 - m_AV_A1 ) Consequently,

m_AV_A1 + m_BV_B1 = m_AV_A2 + m_BV_B2

_____________________________________________________

In general, in a system of colliding bodies, the sum of the components of momentum along any direction remains unaltered during collision. Consequently, the total momentum of an isolated system with no external forces acting on it is constant in magnitude and direction.

Elastic and inelastic collisions. Although momentum is always conserved in a collision, the same is not true of kinetic energy. If the total kinetic energy does remain constant in a collision, the collision is called completely elastic. If not, it is called inelastic. If the colliding bodies stick together and move as a unit after the collision, the collision is called completely inelastic. The only completely elastic collisions known are those of atomic and subatomic particles. However, the collisions of many objects, billiard balls for example, are very nearly completely elastic.

Coefficient of Restitution. For any direct, central impact between two bodies (e.g. spheres) A and B , the coefficient of restitution e is defined as

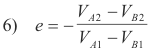
where

V_A1 , V_B1 = the velocities of bodies A and B before impact

V_A2 , V_B2 = the velocities of bodies A and B after impact

For a perfectly elastic collision, e = 1. For an inelastic collision, 0 < e <1. It is assumed that the velocities are all co-linear i.e. that the bodies are both initially and finally moving in the same or opposite directions.

Derivation. Assume that two spheres A and B traveling either directly toward each other or directly away from each other collide in a direct, central impact that is perfectly elastic. Then the total kinetic energy of the two spheres before impact is equal to the total kinetic energy after impact i.e.

Furthermore, the total momentum of the two spheres before impact is equal to the total momentum after impact i.e.

where we note that 8) is a scalar equation (not a vector equation), the V’s representing scalar quantities.

Rearranging equations 7) and 8) we get

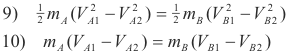
If we now divide 9) by 10) we obtain

or, rearranging,

From this equation we can see that the coefficient of restitution

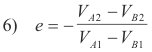
is equal to one for a perfectly elastic collision, providing the motivation for the definition. For an inelastic collision it is a number between 0 and 1.

References

Schaum. College Physics.

Sears, Zemansky. University Physics.

Semat, Katz. Physics.