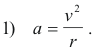
Website owner: James Miller
Centripetal force and centripetal acceleration of bodies moving in uniform circular motion
If we tie an eight ounce ball to the end of a cord and whirl it in a circle we know from experience that the ball will exert a force on the cord in the form of a tension and the faster we whirl the object, the larger will be the force. In 1543 Copernicus published his theory that the earth and other planets revolved about the sun in circular orbits. Such a theory would naturally call to mind the idea of an object being whirled about on a cord and give rise to the question of what force constrained a planet to a circular orbit. Newton later answered that question with his postulate of the existence of a general attractive force existing between any two material objects in the universe i.e. his Law of Universal Gravitation.
We will now consider the laws ruling the motion of a body moving in a circle at a constant speed. Suppose we have a cord tied to an object and we whirl the object about in such a way that it slides in a circular path at a constant speed on a frictionless horizontal plane (we consider a horizontal path to eliminate the effects of gravity). Given the mass m of the object, the radius r of the circular path, and the speed v of the object, we wish to know what force F is exerted on the object in the form of tension on the string.
Newton’s First Law of Motion states: A body at rest will remain at rest and a body in motion will remain in motion at constant speed in a straight line, as long as no unbalanced force acts on it. From Newton’s First Law we understand that any object moving in a circle must have a force acting on it or else it would move in a straight line. Furthermore this force must act towards the center of the circle or else there would be a component of velocity in the direction of its path and its speed would change. The only effect of this force directed towards the center of the circle is to change the direction of the motion of the object. The law that gives the force on the object is Newton’s second law, F = ma, where F is the applied force, m is the mass of the object and a is the acceleration towards the center of the circle caused by the force. In fact, we can show that the acceleration towards the center of the circle experienced by the object is a function of only the two variables v and r and is given by the formula
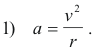
Given values for v and r we can compute the acceleration a and then compute the force F on the object from the formula F = ma.
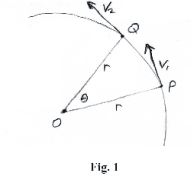
Derivation of the formula a = v2/r. Consider Fig. 1 which shows the velocity of the body at points P and Q. At P it has velocity V = V1 and at point Q it has velocity V = V2 . Here V is a vector quantity which has a constant magnitude v. The change in velocity ΔV is given by the vector difference V2 - V1. If Δt is the time required to go from P to Q, then the average acceleration Aave of the body is given by
![]()
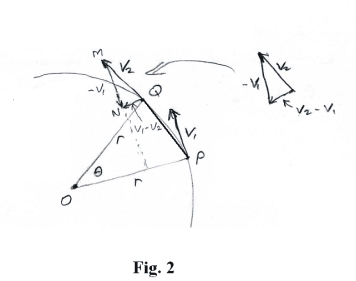
Considering now Fig. 2, we shall show that triangle MNQ is similar to triangle OPQ.. To do this we will employ the following theorem from Euclidean geometry:
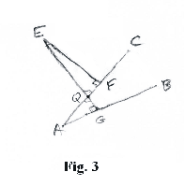
Theorem 1. Given:
![]() BAC. See Fig. 3.
From point E draw perpendiculars EF and
EG to AC and AB respectively. Then
BAC. See Fig. 3.
From point E draw perpendiculars EF and
EG to AC and AB respectively. Then
![]() E =
E =
![]() A.
A.
This theorem is easily proven since
![]() AQG =
AQG =
![]() EQF and thus ΔAQG is
similar to ΔEFQ.
EQF and thus ΔAQG is
similar to ΔEFQ.
We now note in Fig. 2 that MN is perpendicular to OP and MQ is perpendicular to OQ so from
Theorem 1 it follows that
![]() θ of Δ OPQ is equal to
θ of Δ OPQ is equal to
![]() M of
ΔMNQ. Since both triangles OPQ and MNQ are isosceles
triangles, it follows that they are similar.
M of
ΔMNQ. Since both triangles OPQ and MNQ are isosceles
triangles, it follows that they are similar.
Denote the magnitude of V1 by v and the magnitude of ΔV =V2 - V1 by Δv. Then
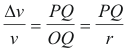
Dividing both sides by Δt and multiplying both sides by v, we obtain
![]()
Denoting the magnitude of the average acceleration by
![]() , we obtain
, we obtain
![]()
To find the instantaneous acceleration a, we take the limit of
![]() as Δt approaches zero: The points
P and Q approach each other and the chord PQ approaches the length of the arc PQ. The distance
PQ can be replaced by vΔt. Substituting these values into 2), we obtain
as Δt approaches zero: The points
P and Q approach each other and the chord PQ approaches the length of the arc PQ. The distance
PQ can be replaced by vΔt. Substituting these values into 2), we obtain
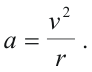
When the angle θ is very small, the vector ΔV is perpendicular to the velocity V1 and is directed toward the center of the circle.
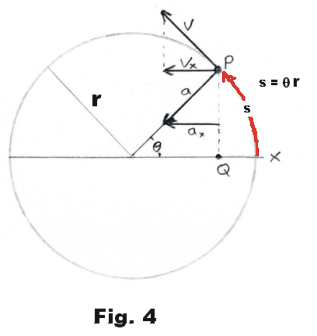
A second simpler method for deriving the formula a = v2/r. There is a much simpler method for deriving the formula using differential calculus. In Fig. 4, s = θr, where s is the distance on the circle from the x-axis to point P, θ is the angle in radians from the x-axis to point P and r is the radius of the circle. The x and y coordinates of point P are given by
1) x = r cos θ
2) y = r sin θ
Now s = vt and θ = s/r, so θ = vt/r where v is the speed i.e. magnitude of velocity V. The above equations then become
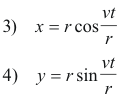
which constitute parametric equations giving the x and y coordinates of the body P as a function of time t. Differentiating 3) and 4) with respect to time gives
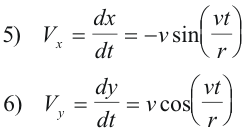
Differentiating 5) and 6) with respect to time, we get the acceleration
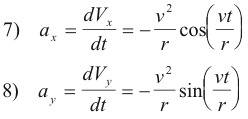
The acceleration a is thus a vector of magnitude v2/r directed in toward the center of the circle.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life