Photometry, Steradian, Intensity of a light source, Candlepower, Lumen, Illuminance, Photometer

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Photometry, Steradian, Intensity of a light source, Candlepower, Lumen, Illumination, Photometer

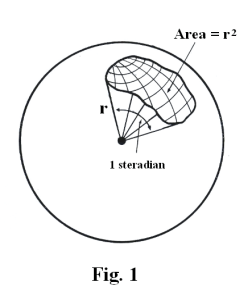
Steradian. Given a sphere of radius r, a steradian is a unit solid angle that subtends an area of r² on the surface of the sphere. See Fig. 1. In a sphere of one foot radius, a steradian would correspond to a solid angle that subtended an area of one square foot on the surface of the sphere. Since the total area of a sphere is 4πr², there are 4π steradians in a sphere.

The concept of steradian is defined in analogy to the definition of a radian. A radian is a unit angle corresponding to a length of one radius on the circumference of a circle. A steradian is a unit of solid angle (or spherical angle) corresponding to an area of r² (one radius squared) on a sphere.

Intensity of a light source. The intensity or strength of a light source is measured in candles. Originally an actual candle, made in a specified way, was used as a standard with the light from the candle flame providing a measure of an intensity called one candle. This definition was dropped and now a source intensity of one candle is defined as the luminous flux contained within a solid angle of one steradian issuing from a 1/60 of a square centimeter opening in a hollow enclosure maintained at a temperature of molten platinum. The quantity of light flux (luminous flux) issuing from a uniform point source of 1 candle intensity through a solid angle of 1 steradian is called a lumen. Thus the amount of illumination falling on a surface 1 foot from a 1-candle light source is 1 lumen per square foot. A 1-candle source, radiating equally in all directions, thus issues a total of 4π lumens of luminous flux.

The intensity of a light source is called its candlepower.

The total luminous flux F emitted by a point source of intensity I is

1) F = 4πI

where F is in lumens and I is in candles.

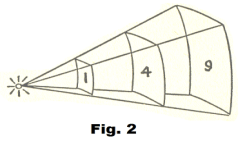
Illumination on a surface. The illumination E on a surface is the density of the light flux incident on the surface i.e. the amount of light per unit area. It diminishes as the square of the distance from the source. A given amount of flux is spread out over a larger and larger area as one gets further from the source. If one envisions spheres of radii 1 foot, 2 feet, and 3 feet centered on a light source, the light flux that passes through 1 ft² on the first sphere will pass through 4 ft² on the second sphere and through 9 ft² on the third sphere [the total areas of the spheres are 4π(1)², 4π(2)², and 4π(3)²]. See Fig. 2.

The illumination on a spherical surface of radius r centered on a point source of intensity I is given by

2) E = I/r²

If r is in feet, the illumination will be in lumens per square foot and if it is in meters, the illumination will be in lumens per square meter.

Let us now consider light incident at an angle on an infinitesimal element of plane surface ΔA which we assume is located at a distance r from a point source of intensity I. The illumination on such an element of surface is given by

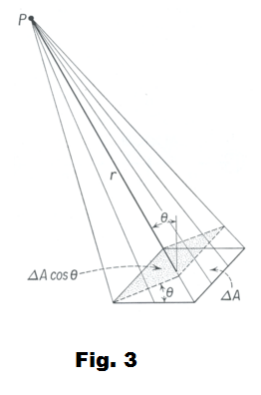
where θ is the angle between the ray of light and the normal to the surface.

Proof. Suppose that a light source of luminous intensity I is located at a distance r from a small element of surface of area ΔA, as shown in Fig. 3, and that the line joining the point source P to ΔA makes an angle θ with the normal to the area element. The solid angle Δω subtended by ΔA at P is given by

The luminous flux ΔF contained in the solid angle Δω is

5) ΔF = I Δω

Substituting 4) into 5) gives

and the illumination E of the surface is

Measurement of the intensity of a light source. We measure the intensity of a light source by comparing its intensity with that of a standard light source using an instrument called a photometer and employing the following principle:

Principle of photometry. The luminous intensities of two sources I₁ and I₂ producing equal illuminance E on a screen are directly proportional to the squares of their distances, r₁ and r₂ respectively, from the screen. In other words, since

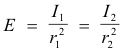
we have the relationship

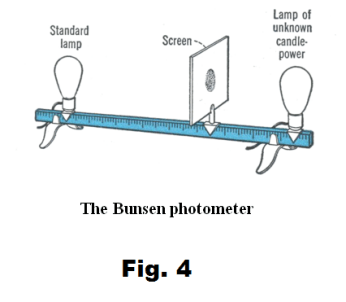
The Bunsen, or grease spot, photometer. The Bunsen photometer, sometimes called the grease spot photometer, consists of a white sheet of paper with a translucent grease spot in its center placed on a meter stick between a standard lamp and a lamp of unknown candlepower. See Fig. 4. The paper is moved back and forth along the meter stick until it is equally illuminated on both sides. At this point the grease spot practically disappears. We then measure the distance r₁ from the Standard lamp to the screen and the distance r₂ from the lamp of unknown intensity to the screen and substitute into 8) above. I₁ is the intensity of the standard lamp and we solve for I₂.

Joly, or paraffin-block, photometer. The Joly, or paraffin-block photometer consists of two paraffin blocks such as one can buy in a grocery store separated by a thin sheet of metal (e.g. tin foil). In a darkened room set a standard lamp and a lamp of unknown candlepower about five feet apart and hold the double paraffin block photometer between them. The light from either side is transmitted by the paraffin but is stopped by the metal. One observes the edges of the blocks. The edge of one block will be brighter than the other and by adjusting the position of the photometer one finds a position in which both sides are of equal brightness. The distances to the blocks are then measured and the calculations are made as with a Bunsen photometer.

References.

Dull, Metcalfe, Brooks. Modern Physics.

Schaum. College Physics.

Sears, Zemansky. University Physics.

Semat, Katz. Physics.

Bennett. Physics (COS)

Freeman. Physics Made Simple.