Origin of the concept of irrational numbers

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

ORIGIN OF THE CONCEPT OF IRRATIONAL NUMBERS

Origin of the concept. The origin of the concept of an irrational number lies in the following fact discovered by the ancient Greeks.

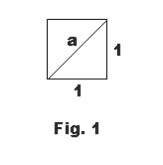
Fact. In a square with sides of unit length there is no rational number equal to the length of its diagonal.

Proof. Consider a square with sides of length 1 and a diagonal of length a. See Fig. 1. According to the Pythagorean Theorem

a² = 1² + 1² = 2 .

But there is no rational number whose square is equal to 2. We prove this as follows:

A rational number is a number that can be written as the quotient of two integers. Thus we wish to prove that there is no quotient p/q whose square is equal to 2 where p and q are positive integers.

Prove. There does not exist two integers p and q, one of which is odd, for which (p/q)² = 2.

Here p and q cannot both be even numbers, for if they were both could be divided by 2 and the fraction could be reduced to lower terms. Hence either p or q is an odd number.

Suppose there are positive integers p and q such that (p/q)² = 2 . If (p/q)² = 2, then

1) p² = 2q²

Thus p² is an even number since twice any number is an even number i.e. the factor 2 in 2q² reveals it as even. But if p² is an even number then p must also be an even number. (Why? The square of any odd number is also odd and if p were odd its square would be odd). Since p is even let b = p/2. Then

2) p² = 4b²

From 1) and 2) we then have

3) 2q² = 4b²

4) q² = 2b²

Thus q² is even and q must also be even. Thus, based on our original suppositions, we have deduced that both p and q are even. But we already know that either p or q must be odd.. This contradiction proves that there are no positive integers p and q such that (p/q)² = 2 .

Prove. The square of any odd number is odd.

Proof. The odd numbers are given by the algorithm

2n + 1 where n = 0, 1, 2, ....

The square of an odd number is given by

(2n + 1)² = 4 n² + 4n + 1

which must be odd since 4 n² + 4n is even.

Q. What is the significance of the fact that there is no rational number that gives the length of the diagonal of a square with unit sides?

A. A rational number, defined as a quotient of two integers, is simply a devise invented by man for designating continuous quantities. Man came up with this idea as a technique for naming any continuous quantity. The significance of the above fact is simply that this devise of using the quotient of two integers for naming continuous quantities is incapable of naming some quantities. Those quantities that it is unable to name are the irrational numbers. Th rational numbers plus the irrational numbers constitute the real numbers.

The irrational numbers

Fact. The square roots of all natural numbers that are not “perfect squares” (i.e. the square of some positive integer) are irrational numbers. Thus, just as there is no rational number whose square is 2, there is no rational number whose square is 3, 5, 6, 7, 8 or any integer that is not a perfect square. Consequently, while the square roots of 1, 4, 9, 16, 25, 36, etc. are rational numbers, the square roots of 2, 3, 5, 6, 7, 8, 10, etc are all irrational numbers. In the same way, the cube roots of natural numbers that are not perfect cubes are all irrational numbers.

We shall prove the above assertion for the natural number 5 i.e. we shall prove that there is no quotient of two integers p/q whose square is 5. Before presenting the proof, we note the following:

1) The unique factorization theorem of arithmetic states:

Unique factorization theorem. Any positive integer greater than 1 is a prime or can be expressed as a product of primes. Except for the order of the factors, this expression is unique.

Syn. Fundamental theorem of arithmetic

Examples. 12 = 2∙2∙3, 84 = 2 ∙2 ∙3 ∙7

2) A consequence of the unique factorization theorem is that if a natural number p is expressed as a product of its primes, then a factorial representation of p² will contain the same primes with each prime occurring twice as many times. This means that every prime factor of p² occurs an even number of times. For example,

84 = 2 ∙2 ∙3 ∙7 and 84² = 2² ∙2² ∙3² ∙7²

The proof is as follows: Assume that there is a rational number p/q whose square is 5; i.e. assume that

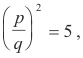
where p and q are natural numbers. Under this assumption

p²= 5q².

Now, from 2) above, we know q² must contain 5 as a factor an even number of times, if it contains it at all. Consequently, 5q² must contain 5 as a factor an odd number of times. Also, from 2) above we know that p² must contain 5 as a factor an even number of times, if it contains it at all. However, if p² were really equal to 5q² that would imply that it contained the factor 5 an odd number of times, a contradiction of known fact. Thus the supposition that there is a quotient of two integers p/q whose square is 5 is proved false.

Sums and products of irrational and rational numbers. It can be shown that the sum of a rational number and an irrational number is an irrational number. It can also be shown that the product of a rational and an irrational number is an irrational number. Thus and are irrational numbers.

Decimal representation of rational and irrational numbers.

Theorem 1. The rational numbers are precisely those decimal numbers that either terminate or are periodic.

One can easily see that a terminating decimal number such as 3.23 is a rational number since it is just another way of writing 323/100, a quotient of two natural numbers. Other rational numbers repeat. Example: 2/3 = 0.66666 ... where the 6's repeat indefinitely and 24/55 = 0.4363636 ... where the block 36 repeats indefinitely.

Theorem 2. The irrational numbers are precisely those infinite decimals that are not repeating.

Theorem 3. An irrational number can be approximated to any desired degree of accuracy by a rational number.

References

Ross R. Middlemiss. Algebra for College Students.

Richard Courant, Herbert Robbins. What is Mathematics?

Hawks, Luby, Touton. Second-Year Algebra