Prove: Let f(z) is analytic at z₀ and (z₀) 0. Then the under the mapping w = f(z) the tangent at z₀ to any curve C passing through z₀ is rotated through the angle arg (z₀).

Proof. See Fig. 1. As a point moves from z₀ to z₀ + Δz along C, the image point traces out C' in the w plane, going from w₀ to w₀ +Δw. Assume that the curves C and C', are defined parametrically with t as the parameter. Then corresponding to the path z = z(t) [or x = x(t), y= y(t)] in the z plane, we have the path w = w(t) [or u = u(t), v = v(t)] in the w plane.

The derivatives dz/dt and dw/dt represent tangent vectors to corresponding points on C and C'.

Now

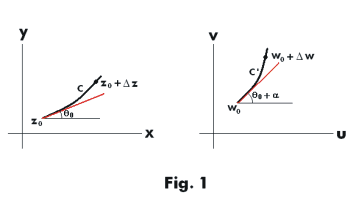
At points z₀ and w₀, we have

Let

Equation 1) then becomes

Thus

which is what we wished to prove.