Point, one-to-one, inverse transformations. Jacobian. Conformal mapping. Riemann�s mapping theorem. Successive transformations. Linear, bilinear, fractional, Mobius, Schwartz-Christoffel transformations.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Point, one-to-one, inverse transformations. Jacobian. Conformal mapping. Riemann’s mapping theorem. Successive transformations. Linear, bilinear, fractional, Mobius, Schwartz-Christoffel transformations.

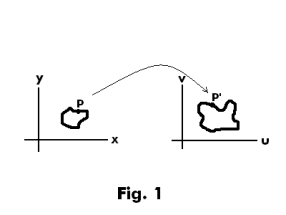
Point transformations. The system

u = u(x, y)

v = v(x, y)

represents a function that assigns to every number pair (x, y) another number pair (u, v). The number pairs (x, y) and (u, v) can be viewed as representing points in a plane and the system can be viewed as defining a point transformation that maps a point (x, y) in an xy-coordinate system into a point (u,v) in a uv-coordinate system. See Fig. 1. In the same way the system

u = u(x, y, z)

v = v(x, y, z)

w = w(x, y, z)

represents a function that assigns to every number triple (x, y, z) another number triple (u, v, w). The number triples (x, y, z) and (u, v, w) can be viewed as representing points in three-dimensional space and the system can be viewed as defining a point transformation that maps a point (x, y, z) in an xyz-coordinate system into a point (u, v, w) in a uvw-coordinate system. Generalizing on this idea the system of equations

u₁ = u₁(x₁, x₂, ... , x_n)

u₂ = u₂(x₁, x₂, ... , x_n)

.....

u_m = u_m(x₁, x₂, ... , x_n)

assigns a point (u₁, u₂, ... , u_m) in m-dimensional space to a point (x₁, x₂, ... , x_n) in n-dimensional space. The domain is some specified point-set in n-dimensional space and the range is some point-set in m-dimensional space. It can be viewed as defining a point transformation from n-space into m-space.

Syn. mapping, point transformation, transformation

Continuity and differentiability of point transformations. A point transformation is said to be continuous if the defining functions u₁, u₂, ... , u_n are continuous. It is said to be differentiable if these functions are differentiable. It is continuously differentiable if these functions have continuous partial derivatives.

One-to-one transformations. Let a point transformation map some region R into a region R'. If every point of R is mapped into a different point of R', no two points of R being mapped into the same point, the mapping is one-to-one. In a one-to-one mapping there is established a one-to-one correspondence between the points in R and R' with each point in region R being mapped into its correspondent in R'.

Inverse of a point transformation. A point transformation T can have an inverse transformation T^-1 if and only if T maps in a one-to-one fashion. Let T be a one-to-one transformation mapping each point of a region R into some point in region R'. Then the inverse transformation T^-1 maps each point of R' into that point in R that was imaged into it under transformation T. If a point transformation

u = u(x, y)

v = v(x, y)

is one-to-one then there exists an inverse transformation

x = x(u, v)

y = y(u, v)

that maps each point (u, v) back into its correspondent point (x, y).

Jacobian of a transformation. The Jacobian of the point transformation

u₁ = f₁(x₁, x₂, ... , x_n)

u₂ = f₂(x₁, x₂, ... , x_n)

.....

u_n = f_n(x₁, x₂, ... , x_n)

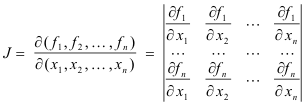
Example. For the point transformation

u = f₁(x, y)

v = f₂(x, y)

the Jacobian is given by

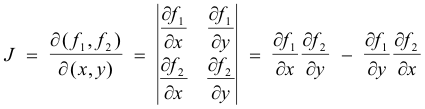
Physical interpretation of the Jacobian. Consider the point transformation

u = u(x, y)

v = v(x, y)

Assume the transformation maps a small area ΔA into ΔA'. Then

where J is the Jacobian of the transformation.

Condition for a point transformation to be one-to-one. A point transformation is one-to-one at a point if the Jacobian does not vanish at the point. A point transformation is one-to-one in a specified region if the Jacobian of the transformation does not vanish within the region. If a transformation is one-to-one an inverse transformation exists. If an inverse exists, the Jacobian of the inverse transformation is the reciprocal of the Jacobian of the transformation.

Significance of the sign of the Jacobian. Consider a mapping at a point (x₀, y₀) where the Jacobian is not zero and the mapping is thus, at least locally, one-to-one. If C is a small closed curve encircling the point (x₀, y₀) in the xy plane the image of C will be a small closed curve C' encircling the point (u₀, u₀), the image of (x₀, y₀), in the uv plane. Let the point (x, y) goes around C in the counterclockwise direction. The image point (u, v) will then go around C'. If the Jacobian is greater than zero the image point (u, v) will go around C' in the same direction that point (x, y) goes around C. If the Jacobian is less than zero, it will go around in the opposite direction.

General mapping of w = f(z). We represent the general function of a complex variable by w = f(z). If z = x + yi, on expansion of f(x + yi) we obtain w = u + iv where

1) u = u(x, y)

v = v(x, y)

i.e. it is a special case of a 2-space to 2-space mapping. The function f(z) is called the mapping function. A complex function f(z) may have multiple values at only some points in the z plane and single values at the rest. If it has multiple values at any point in the z plane it is regarded as being multiple-valued.

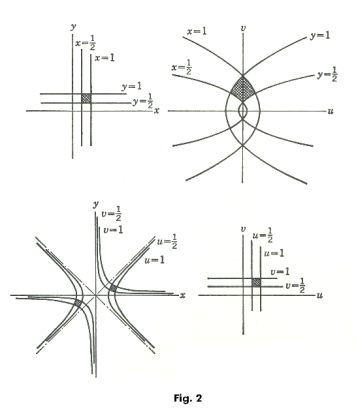
Let us take a very simple function of a complex variable and inquire how it maps figures, areas, points. Let us pick the function w = z² and ask the following question: Into what does the function map the rectangular area in the z plane bounded by the lines x = 1/2, x = 1, y = 1/2, y = 1 shown in the top left of Fig. 2? We answer the question by asking what it maps the lines x = 1/2, x = 1, y = 1/2, y = 1 into. To answer that question we proceed as follows: We expand the function w = z² = (x + iy)² obtaining

w = (x + iy)² = (x² - y²) + 2ixy

w = u + iv

where

2) u = x² - y²

v = 2xy

which corresponds to system 1) above. Into what does system 2) map the line x = 1? We obtain the answer by replacing x with 1 in system 2) giving

3) u = 1 - y²

v = 2y ,

a parametric system with y as parameter. Each value of y corresponds to some point on the line x = 1. Eliminating y from system 3) gives

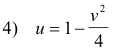
which is the parabola shown in the top right of Fig. 2. In the same way we map the other lines x = 1/2, y = 1 and y = 1/2. The top right figure in Fig. 2 shows the area that the rectangle maps into.

We can ask another question: What system of lines does the line x = c₁ map into, regarding the constant c₁ as a parameter? To answer that question we replace x with c₁ in system 2) giving the parametric system

5) u = c₁² - y²

v = 2c₁y .

We then eliminate y from that system to get

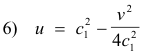
which defines a family of parabolas having the origin of the w plane as focus, the line v = 0 as axis, and all opening to the left. In the same way we can ask what system of lines the line y = c₂ maps. We proceed in the same way. We substitute c₂ for y in system 2) to obtain the parametric equations

7) u = x² - c₂²

v = 2c₂x

and then eliminate x to obtain

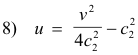
which is the equation of a family of parabolas having the origin as focus, the line v = 0 as axis, and all opening to the right.

Let us now ask a different question. Let us ask this question: What region or regions in the xy plane map into the rectangular area in the uv plane bounded by the lines u = 1/2, u = 1, v = 1/2, v = 1 shown in the bottom right of Fig. 2? We proceed in a similar way. We ask ourselves what line or lines map into the line u = 1. The answer is found by replacing u with 1 in system 2). It is the hyperbola

x² - y² = 1

in the xy plane. What line or lines map into the line v = 1? We replace v with 1 in system 2) to get

xy = 1/2 .

We obtain the lines in the xy plane imaging into the lines u = 1/2 and v = 1/2 in the same way and the areas in the xy plane that map into the specified rectangular area of the uv plane are shown in the bottom left of Fig. 2.

Again we can ask the question: What system of lines in the xy plane map into the line u = k₁ in the uv plane? We substitute k₁ for u in system 2) to get

x² - y² = k₁ ,

a system of rectangular hyperbolas. What system of lines in the xy plane map into the line v = k₂ in the uv plane? We substitute k₂ for v in system 2) to get

xy = k₂/2 ,

another system of rectangular hyperbolas.

Suppose we ask the following question: Into what does system 2) map the line

9) y = 2x + 1

in the xy plane? ? The answer is found by solving system 2) and equation 9) i.e. the following system

y = 2x + 1

u = x² - y²

v = 2xy ,

simultaneously, eliminating x and y.

After going through the algebra the answer is found to be

16u² + 24uv + 9v² + 12u - 16 v = 4

which is the equation of a parabola in the uv plane.

Jacobian of an analytic function of a complex variable.

Theorem. Consider a general function of a complex variable w = f(z) where z = x + yi. On expansion of f(x + yi) we obtain w = u + iv where

u = u(x, y)

v = v(x, y) .

In a region where the function f(z) is analytic, the Jacobian of the transformation w = f(z) is given by

Proof

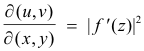
It follows that the transformation is one-to-one in regions where f '(z) ≠ 0. Points where f '(z) = 0 are called critical points.

Def. Conformal mapping. A mapping that preserves angles in both magnitude and in sense. Suppose that under the transformation

u = u(x, y)

v = v(x, y)

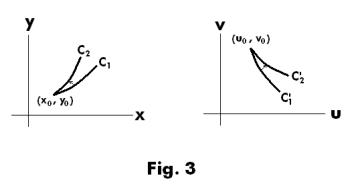
point (x₀, y₀) in the xy plane is mapped into point (u₀, v₀) in the uv plane. Let curves C₁ and C₂ emanating from (x₀, y₀) be mapped into curves C'₁ and C'₂ emanating from point (u₀, v₀). See Fig. 3. Then if the transformation is such that the angle at (x₀, y₀) between C₁ and C₂ is equal to the angle at (u₀, v₀) between C'₁ and C'₂ both in magnitude and sense, the transformation or mapping is said to be conformal at (x₀, y₀). A mapping that preserves the magnitudes of angles but not necessarily the sense is called isogonal.

Theorem 1. Let f(z) is analytic at z₀ and f '(z₀) ≠ 0. Then the under the mapping w = f(z) the tangent at z₀ to any curve C passing through z₀ is rotated through the angle arg f '(z₀). See Fig. 4.

Proof

Theorem 2. If f(z) is analytic and f '(z) ≠ 0 in a region R, then the mapping w = f(z) is conformal at all points of R.

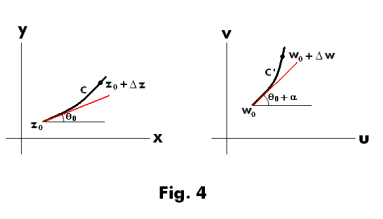
Theorem 3. In a mapping defined by an analytic function w = f(z), infinitesimal segments, regardless of their direction, are magnified by a factor |f '(z) | which depends only on the point from which they are drawn.

In a conformal mapping, infinitesimal configurations in the neighborhood of a point z₀ in th z plane map into similar infinitesimal configurations in the w plane and are magnified (or reduced) by an amount given approximately by |f '(z₀)²|, called the area magnification factor (or simply the magnification factor). Since an infinitesimal configuration and its image conform to each other in the sense of being approximately similar, the mapping is called conformal. This is not true, however, for large figures, which may bear little or no resemblance to their image.

Riemann mapping theorem. Any non-empty simply connected open set in the plane, other than the whole plane, can be mapped one-to-one and conformally onto the interior of a circle.

James/James. Mathematics Dictionary

While Riemann’s mapping function asserts the existence of a function, it does not actually produce the function.

Fixed or invariant points of a transformation. Suppose we superimpose the w plane on the z plane so that the coordinate axes coincide and there is essentially only one plane. Then we can think of the transformation w = f(z) as mapping certain points of the plane into other points. Points that are mapped into themselves i.e. points at which f(z) = z, are called the fixed or invariant points of the transformation.

Example. The fixed or invariant points of the transformation w = z² are the solutions of z² = z i.e .z = 0, 1.

******************************

Some general transformations

The elementary transformations. Many complex transformations reduce to a combination of one or more of the following four transformations. We will call them the elementary transformations. In the these transformations it is convenient to think of the w plane as superimposed on the z plane, coordinate axes coinciding, so there is essentially one plane. These operations of translation, rotation, stretching and inversion then represent changes in the same plane.

1. Translation.

w = z + β

where β is complex i.e. addition of vector z to constant vector β.

Effect: Translation of a figure in the direction of vector β by a distance |β|

2. Rotation.

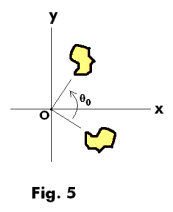
where θ₀ is real.

Effect: Rotation of a figure about the origin by the angle θ₀. See Fig. 5. If θ₀ > 0 the rotation is counterclockwise and if θ₀ < 0 the rotation is clockwise.

This transformation causes the entire z plane to be rotated about the origin by an angle of θ₀.

3. Stretching (or contracting).

w = az

where a is real and positive i.e. multiplication of vector z by positive scalar a.

Effect: Multiplies the modulus of each point in the z plane by a and, consequently, effects a scale change equivalent to stretching or contracting the z plane uniformly about z = 0. If a > 1, the effect is stretching. If a < 1 it is contracting.

● This transformation maps straight lines into straight lines, circles into circles, and, in general, conics into conics of the same type.

4. Inversion.

w = 1/z

Effect: If a vector z has a magnitude r and amplitude α, then 1/z will have a magnitude 1/r and an amplitude -α. This is evident from

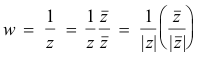
We see that w is a vector of magnitude 1/|z| in the direction of vector . Thus the effect on a figure of an inversion will be a contracting (or stretching) in the direction of z and a reflection about the real axis.

This transformation does all of the following:

(1) preserves circles not passing through the origin

(2) maps circles passing through the origin into straight lines

(3) maps straight lines not containing the origin into circles passing through the origin

(4) maps straight lines passing through the origin into straight lines passing through the origin

(5) leaves the unit circle |z| = 1 unchanged (maps it into itself)

(6) interchanges the interior and exterior of the circle |z| = 1 .

Theorem 4. The elementary transformations 1- 4 (translation, rotation, stretching, inversion) map straight lines into straight lines and circles into circles, with the exception of the inversion transformation, which may in some cases map straight lines into circles and circles into straight lines.

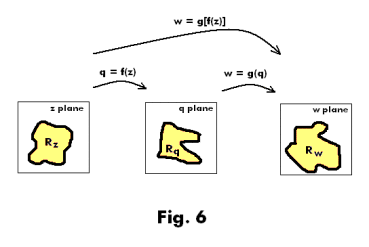
Successive transformations. If q = f(z) maps region R_z of the z plane into region R_q of the q plane and w = g(q) maps region R_q of the q plane into region R_w of the w plane, then w = g{f(z)] maps region R_z of the z plane into region R_w of the w plane. See Fig. 6. The functions f and g define successive transformations from one plane to another which are equivalent to a single transformation. The ideas are easily generalized.

The linear transformation. The transformation

w = αz + β

where α and β are complex constants, is called a linear transformation. The linear transformation is a combination of the elementary transformations translation, rotation and stretching as can be seen if we note that α can be expressed as

which is a combination of stretching and rotation. The linear transformation w = αz + β is thus equivalent to the successive transformations

performed in that order.

Theorem 5. The linear transformation

w = αz + β

preserves straight lines and conic sections.

The bilinear, linear fractional or Mobius transformation. The transformation

where a, b, c, d are complex numbers is called a bilinear, linear fractional or Mobius transformation.

Theorem 6. The bilinear transformation can be expressed as a succession of the four elementary transformations translation, rotation, stretching and inversion.

Proof

Theorem 7. The bilinear transformation maps straight lines into either straight lines or circles. It maps circles into either straight lines or circles.

In a manner analogous to the way in which three points are needed to determine a triangle, two points are needed to determine a line in space and three points are needed to determine a plane in space a particular bilinear mapping

is determined by the mapping of any three points z₁, z₂ and z₃ in the z plane, that is, by a mapping

z₁ w₁

z₂ w₂

z₃ w₃.

If we are given the mapping for three points we can determine the values of the constants a, b, c and d of 1) by substituting these conditions into 1) and solving the resulting system.

_________________________________________________________________

Example. Find a linear transformation that maps points z = 0, - i, - 1 into points w = i, 1 , 0 respectively.

Solution. We substitute the values of w and z for the three given points into

to get the three equations

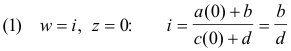
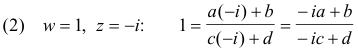
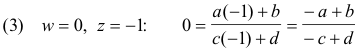
and then solve these equations.

From (3) we get

(4) a = b

From (1) and (4) we get

(5) d = b/i = -ia

From (2), (4) and (5) we get

(6) c = ia

Then

_____________________________________________________

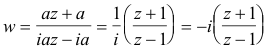
There is a way of solving the above problem that is often simpler that makes use of the fact that if w₁, w₂, w₃, w₄ are, respectively, the images of z₁, z₂, z₃, z₄, then

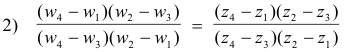
The fraction in the right member

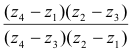
is called the cross ratio or anharmonic ratio of the four numbers z₁, z₂, z₃, z₄.

Theorem 8. The cross ratio of four points z₁, z₂, z₃, z₄ is invariant under a bilinear transformation i.e. if w₁, w₂, w₃, w₄ are, respectively, the images of z₁, z₂, z₃, z₄ under a bilinear transformation, then the cross ratio of w₁, w₂, w₃, w₄ must equal the cross ratio of z₁, z₂, z₃, z₄ , that is

Proof

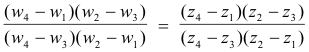
Suppose now that we wish to find the transformation that maps z₁, z₂, z₃ into w₁, w₂, w₃ respectively. If w is the image of a general point z under this transformation, then, according to Theorem 8, the cross ratio of w₁, w₂, w₃ and w must equal the cross ratio of z₁, z₂, z₃ and z_. That is

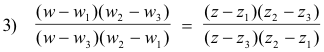
So we simply plug the known values of w₁, w₂, w₃ and z₁, z₂, z₃ into 3) and solve for w in terms of z.

Example. Find a linear transformation that maps points z = 0, - i, - 1 into points w = i, 1 , 0 respectively.

Solution. Substituting the values of z and w into 3) we get

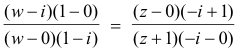
Solving for w, with some algebraic manipulation, we get

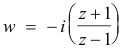
Mapping of a half plane onto a circle

Theorem 9. Let θ₀ be any real constant z₀ be any point in the upper half plane. Then the bilinear transformation

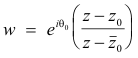
maps the upper half plane in a one-to-one manner onto the interior of the unit circle |w| = 1.

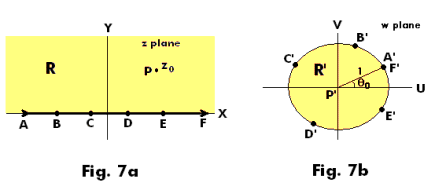
Each point of the x (real) axis is mapped onto the boundary of the circle. See Fig. 7. Points A, B, C, D, E, and F on the axis are mapped into points A', B', C', D', E', and F' on the boundary of the circle. Points A and F, marked by arrows, correspond to points at infinity. As point z moves along the boundary of region R (i.e. along the real axis) from (point A) to (point F), w moves counterclockwise along the unit circle from A' back to A'.

The transformation maps point z₀ into the origin. The angle θ₀ corresponds to point A'. It determines where A' is mapped on the circle.

The Schwartz-Christoffel transformation

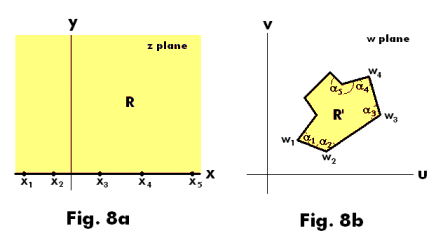
Theorem 10. Consider a polygon in the w plane having vertices at w₁, w₂, ... , w_n with corresponding interior angles α₁, α₂, ... , α_n respectively. See Fig. 8b.

A transformation which maps the upper half plane R of the z plane onto the interior R' of the polygon and the real axis of the z plane onto the boundary of the polygon is given by

where the points x₁, x₂, ... , x_n on the real axis of the z plane are mapped respectively into the points w₁, w₂, ... , w_n of the polygon and A and B are complex constants.

Proof

If one or more of the vertices of the polygon are removed to infinity, a limiting form of the transformation is obtained which maps the upper half of the z plane onto a region bounded by line segments which are images of corresponding segments of the real axis.

We note the following:

● Any three of the points x₁, x₂, ... , x_n can be chosen at will.

● The constants A and B determine the size, orientation and position of the polygon.

● If one removes a point x_i to infinity, the factor of 1] and 2] involving x_i is not present.

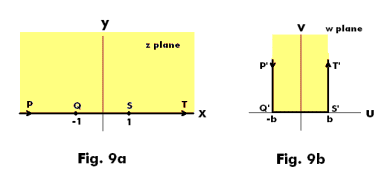
Problem. Determine a function which maps the upper half of the z plane onto the region P'Q'S'T' of the w plane shown in Fig. 9b.

Solution. Let points P, Q, S and T in Fig. 1a map into points P', Q', S' and T' in Fig. 1b. We will consider P'Q'S'T' as a limiting case of a polygon (a triangle) with two vertices at Q and S and the third vertex P or T at infinity.

Using the Schwartz-Christoffel transformation, noting that the angles at Q' and S' are equal to π/2, we have

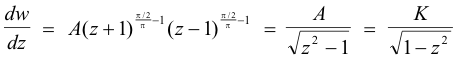
Integrating we get

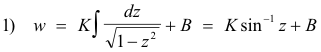
We now determine the values of the constants K and B by substituting into 1) the values z = 1, w = b and z = -1, w = -b.

Substituting z = 1, w = b into 1) we get

2) b = K sin^-1 (1) + B = Kπ/2 + B

Substituting z = -1, w = -b into 1) we get

3) -b = K sin^-1 (-1) + B = -Kπ/2 + B

Solving 2) and 3) simultaneously we get B = 0, K = 2b/π.

Thus

Transformations of boundaries in parametric form

Theorem 11. Let a curve C in the z plane, which may or may not be closed, be defined by the parametric equations

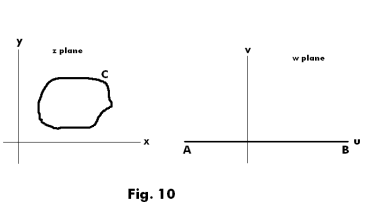
x = f(t)

y = g(t)

where f(t) and g(t) are assumed to be continuously differentiable. Then the transformation

1) z = f(w) + ig(w)

maps the real axis AB of the w plane onto curve C. See Fig. 10.

Proof

The inverse transformation will map curve C onto the real axis AB of the w plane.

Example. Find the transformation that maps the real axis of the w plane onto the ellipse

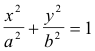
in the z plane.

Solution. A set of parametric equations for the ellipse is given by

x = a cos t

y = b sin t

where a > 0, b > 0. Then by the theorem the required transformation is z = a cos w + ib sin w.

References

Spiegel. Complex Variables. (Schaum)

Wylie. Advanced Engineering Mathematics

Hauser. Complex Variables with Physical Applications