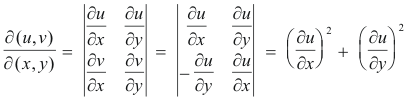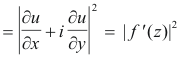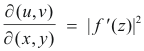
Prove: Let w = f(z), where z = x + yi, which on expansion of f(x + yi) gives w = u + iv where

            u = u(x, y)

            v = v(x, y) .

In a region where the function f(z) is analytic, the Jacobian of the transformation is given by

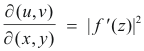
Proof. If f(z) is analytic in a region, the Cauchy-Riemann equations

are satisfied. Thus