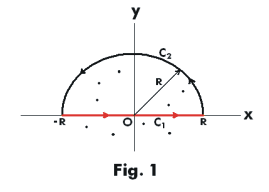
Prove: If f(z) is analytic inside and on a simple, closed curve C , except for a pole of order p at z = a inside C, then

If f(z) is analytic inside and on a simple, closed curve C , except for a zero of order n at z = a inside C, then

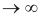
Proof.

Prove: If f(z) is analytic inside and on a simple, closed curve C , except for a pole of order p at z = a inside C, then

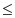
Proof. Since f(z) has a pole of order p at z = a, we have

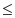
where F(z) is analytic and different from zero inside and on C. We now perform logarithmic differentiation on 1). Taking logarithms, 1) becomes

2)        ln f(z) = ln F(z) - p ln (z - a)

Now taking derivatives of 2) with respect to z we get

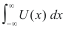
Taking the integral of both sides of 3) we get

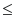
Now

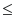
because F'(z)/F(z) is an analytic function inside and on C. Why is this so? Because F'(z) is analytic wherever F(z) is analytic and so F'(z)/F(z) is analytic wherever F(z) is analytic and F(z) is analytic and different from zero inside and on C.

In addition,

by Theorem 1 of this section.

Thus 4) becomes

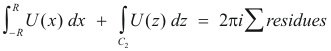
End of Proof.

Prove: If f(z) is analytic inside and on a simple, closed curve C , except for a zero of order n at z = a inside C, then

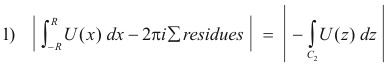
Proof. Since f(z) has a zero of order n at z = a, we have

8)        f(z) = (z - a)ⁿG(z)

where G(z) is analytic and different from zero inside and on C. We now perform logarithmic differentiation on 8). Taking logarithms, 8) becomes

9)        ln f(z) = n ln (z - a) + ln G(z)

Now taking derivatives of 9) with respect to z we get

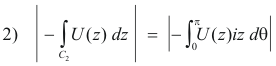
Taking the integral of both sides of 10) we get

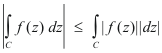
End of Proof.