Prove: If U(z) is a function which is analytic in the upper half of the z plane except at a finite number of poles, none of which are on the real axis, and if zU(z) converges uniformly to zero when z through values for which 0 arg z π, then is equal to 2πi times the sum of the residues at the poles of U(z) that lie in the upper half plane.

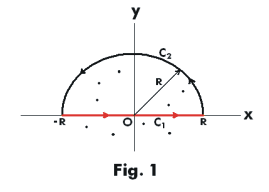
Proof. Let C₁ be the segment -R x R of the x axis and C₂ be the semi-circle z = Re^iθ, center at the origin and radius R large enough to include all the poles of U(z) which lie in the upper half plane. See Fig. 1. By the residue theorem

or

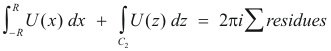
Thus

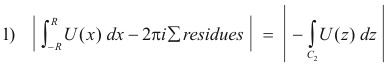
In the integral on the right, let z = Re^iθ, so that dz = Rie^iθdθ = izdθ. Then

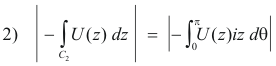
Using the property of line integrals which states

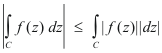
we can write

Thus, from 2) and 3),

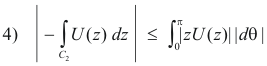
From the hypothesis that |zU(z)| converges uniformly to zero when z and 0 arg z π, it follows that for any arbitrarily small positive quantity, say ε/π, there exists a radius R₀ such that

for all values of z on C₂ whenever R > R₀. Thus for R > R₀

Thus from 4) and 5) we see that if R > R₀

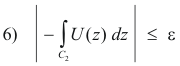
Consequently we can write 1) as

or

References

  Wylie. Advanced Engineering Mathematics