Website owner: James Miller
Method of Residues. Residue theorem. Evaluation of real definite integrals. Cauchy principal value. Summation of series.

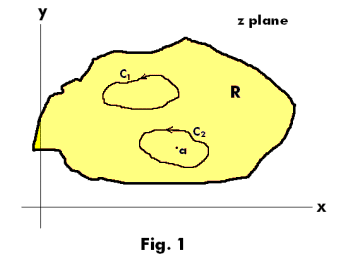
Method of Residues. Let f(z) be analytic in a region R, except for a singular point at z = a, as shown in Fig. 1. Cauchy’s theorem tells us that the integral of f(z) around any simple closed curve that doesn’t enclose any singular points is zero. Thus for a curve such as C1 in the figure
![]()
What is the value of the integral of f(z) around a curve such as C2 in the figure that does enclose a singular point? The answer:
![]()
where a-1 is the coefficient of 1/(z - a) in the Laurent expansion of f(z) about a. The Laurent expansion about z = a is given by
![]()
where
![]()
If we evaluate 3) for k = -1 we get
![]()
The same result can be obtained by taking the integral of f(z) in 2)
![]()
and integrating term by term using the following theorem
Theorem 1. Let C be a simple closed curve containing point a in its interior. Then
![]()
whereby all terms except the a-1 term drop out.
Def. Residue of an analytic function at an isolated singular point. The residue of an analytic function f(z) at an isolated singular point z0 is
![]()
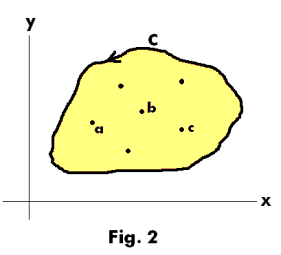
where a-1 is the coefficient of (z - a)-1 in the Laurent expansion of f(z) about z0 and C is a simple closed curve enclosing z0.
Residue theorem. Let f(z) be analytic inside and on a simple closed curve C except at the isolated singularities a, b, c, ... inside C which have residues given by ar, br, cr ... . Then
![]()
See Fig.2.
Calculation of residues
1. Residues at poles. The following theorem gives a simple procedure for the calculation of residues at poles.
Theorem 2. If f(z) has a pole of order m at z = a, then the residue of f(z) at z = a is given by
![]()
if m =1, and by
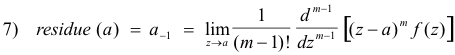
if m > 1.
Note. Formula 6) can be considered a special case of 7) if we define 0! = 1.
Example. Let
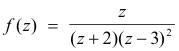
Then f(z) has two poles: z = -2, a pole of order 1, and z = 3, a pole of order 2.
The residue at z = -2 is given by
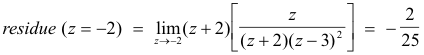
The residue at z = 3 is given by
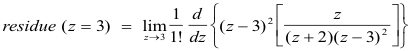
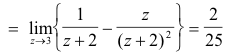
Often the order of the pole will not be known in advance. In this case it is still possible to apply Theorem 2 by taking m = 1, 2, 3, ... , in turn, until the first time a finite limit is obtained for a-1. The value of m for which this occurs is the order of the pole and the value of a-1 thus computed is the residue.
2. Residues at essential points. Residues at essential singularities can sometimes be found by using known series expansions.
Example. In the function f(z) = e-1/z, z = 0 is an essential singularity. Using the known series expansion for eu
![]()
and setting u = -1/z we get the series expansion for e-1/z
![]()
The residue at z = 0 is the coefficient of 1/z and is -1.
Theorem 3. The power series expansion of a function about a point is unique.
The Laurent expansion about a point is unique. Thus if a series expansion of the Laurent type is found by any process, it must be the Laurent expansion.
3. Residues at removable singularities.
Theorem 4. The residue of a function at a removable singularity is zero.
Evaluation of real definite integrals. There are several large and important classes of real definite integrals that can be evaluated by the Method of Residues. We now treat the following types:
Type 1. The integral
![]()
where the integrand R1 is a finite-valued rational
function of sin θ and cos θ for 0
![]() θ
θ
![]() 2π.
2π.
General procedure. Perform the substitution z = eiθ. This substitution transforms integral 8) into the integral
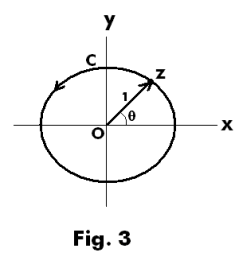
![]()
where R2(z) is a rational function of z and C is the positively-sensed unit circle centered at z = 0 shown in Fig. 3. The residue theorem then gives the solution of 9) as
![]()
where Σ r is the sum of the residues of R2(z) at those singularities of R2(z) that lie inside C.
Details. We perform the substitution z = eiθ as follows: Apply the substitution to
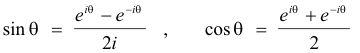
thus transforming them into
![]()
and then substitute these expressions for sin θ and cos θ as expressed in terms of z and z-1 into R1(sin θ, cos θ). Let f(z) be the function obtained from R1(sin θ, cos θ) by the substitution. From z = eiθ we get dθ = dz/iz. Then R2(z) = f(z)/iz. We can then calculate the residues of those singular points of R2(z) that lie within the unit circle by methods described above and the integral is evaluated as
![]()
Type 2. The integral
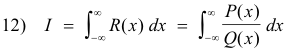
where the integrand R(x) = P(x)/Q(x) is a rational function that has no poles on the real axis and is such that the degree of the polynomial Q(x) in the denominator is at least two greater than the degree of the polynomial P(x) in the numerator.
Theorem 5. If U(z) is a function which is analytic in the upper half of the z plane except at a
finite number of poles, none of which are on the real axis, and if zU(z) converges uniformly to
zero when z
![]() through values for which 0
through values for which 0
![]() arg z
arg z
![]() π, then
π, then
![]() is equal to 2πi times
the sum of the residues at the poles of U(z) which lie in the upper half plane.
is equal to 2πi times
the sum of the residues at the poles of U(z) which lie in the upper half plane.
A function R(x) = P(x)/Q(x) automatically satisfies all the requirements of Theorem 5 if the degree of the denominator exceeds the degree of the numerator by at least two. Thus we have the following corollary.
Corollary 1. If P(x) and Q(x) are real polynomials such that the degree of Q(x) is at least two more than the degree of P(x), and if Q(x) has no real roots, then
![]()
General procedure. We determine the poles from the zeros of Q(x) and then compute the residues at the poles in the upper half plane by the method of Theorem 2 above.
Example. Evaluate the integral
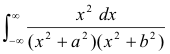
Solution. The integral meets the requirements of Corollary 1. The only poles are at z =
![]() ai,
ai,
![]() bi. Only the poles ai and bi lie in the upper half plane. At z = ai the residue is
bi. Only the poles ai and bi lie in the upper half plane. At z = ai the residue is
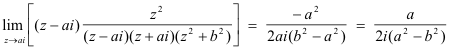
From symmetry it can be seen that the residue at z = bi must be b/2i(b2 - a2). Thus the value of the integral is
![]()
Type 3. The integral
![]()
where the function R(x) = P(x)/Q(x) is a rational function that has no poles on the real axis and the degree of the polynomial in the denominator is at least one greater than that of the polynomial in the numerator.
Solution. Let
![]()
and consider the function R(z)eimz . Let Σ r be the sum of the residues of R(z)eimz in the upper half plane. Then
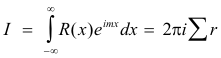
and I1 and I2 are, respectively, the real and imaginary parts of I. In other words,
![]()
![]()
Example. Evaluate
![]()
Solution. Consider the related function
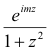
Its only pole in the upper half plane is z = i, and its residue there is
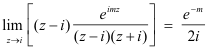
So
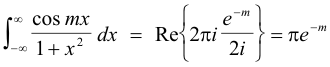
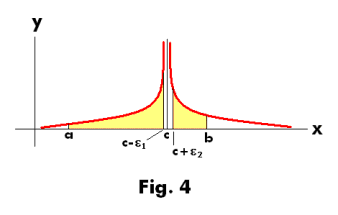
Before proceeding to the next type we need to define the term Cauchy principal value.
The Cauchy principal value of integrals. Let f(x) be a function which is finite at all points of the closed interval [a, b] except at the point x = c, where it becomes infinite. See Fig. 4. Suppose that f(x) is integrable on the intervals [a, c - ε1] and [c + ε2, b] for any positive values of ε1 and ε2. Then we define
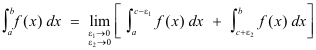
In some cases the above limit does not exist for ε1
![]() ε2 but does exist if we take ε1 = ε2 = ε. In
such a case we define
ε2 but does exist if we take ε1 = ε2 = ε. In
such a case we define
![]()
and call it the Cauchy principal value, or simply principal value, of integral
![]() and
write
and
write
![]()
Example. The following integral
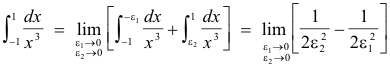
does not exist, however the Cauchy principal value with ε1 = ε2 = ε does exist and equals zero.
Type 4. The integral
![]()
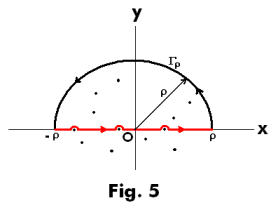
where the associated complex function f(z) is a meromorphic function which may have simple poles on the real axis and which approaches zero uniformly on any circular arc centered at z = 0 as the radius of the arc approaches infinity. See Fig. 5.
Let a function f(z) satisfy the inequality |f(z)| < Kρ when z is on a circular arc Γρ of radius ρ, and let Kρ depend only on ρ so that the inequality holds for all z on Γρ, regardless of the argument of z. If Kρ → 0 as ρ → ∞, then f(z) approaches zero uniformly on Γρ as ρ → ∞.
If ρ is allowed to become sufficiently large all poles in the upper half plane will fall within the contour shown in Fig. 5.
Solution. Consider the associated function f(z)eimz = f(z) cos mx + f(z) sin mx. Let Σ r be the sum of the residues of f(z)eimz at all poles lying in the upper half plane (not including those on the real axis). Let Σ r' be the sum of the residues of f(z)eimz at all simple poles lying on the real axis. Then
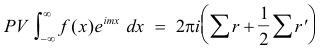
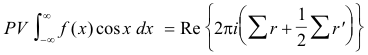
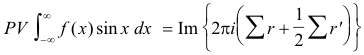
Type 5. The integral
![]()
where Q(z) is analytic everywhere in the z plane except at a finite number of poles, none of which lies on the positive half of the real axis.
Solution. The solution is given by the following theorem:
Theorem. Let Q(z) be analytic everywhere in the z plane except at a finite number of poles, none of which lies on the positive half of the real axis. If |zaQ(z)| converges uniformly to zero when z → 0 and when z → ∞, then
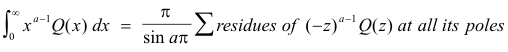
provided arg z is taken in the interval (-π, π).
It should be noted that unless a is an integer, (-z)a-1 is a multiple-valued function which, using the defining formula az = e z ln a, is given by
(-z)a-1 = e (a-1) ln (-z) = e (a-1)[ln |z| + i arg (-z)} -π < arg z
![]() π
π
Type 6. The integral
![]()
where R(z) is a rational function of z which has no poles at z = 0 nor on the positive part of the real axis and k is not an integer.
Solution. To insure convergence of this integral it is necessary that it have the proper behavior at
zero and infinity. It is sufficient that
![]() . In evaluating the
integral we employ the related function z-kR(z) which is a multiple-valued function. The branch
of this function that is used is z-k = e -k(ln |z| + i arg z).
. In evaluating the
integral we employ the related function z-kR(z) which is a multiple-valued function. The branch
of this function that is used is z-k = e -k(ln |z| + i arg z).
Let Σ r be the sum of the residues of z-kR(z) at the poles of R(z). The integral is evaluated by the formula
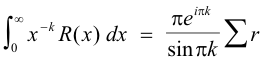
provided z-k = e -k(ln |z| + i arg z).
For types of integrals not covered above, evaluation by the method of residues, when possible at all, usually requires considerable ingenuity in selecting the appropriate contour and in eliminating the integrals over all but the selected portion of the contour.
Special theorems used in evaluating definite integrals. In evaluating definite integrals by the method of residues the following theorems are often useful.
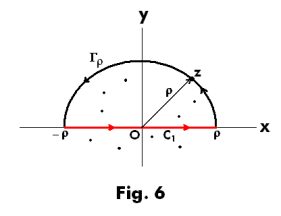
Theorem 1. Let Γρ be a semicircular arc of
radius ρ, in the upper half plane, centered at the
origin. See Fig. 6. If |f(z)|
![]() M/ρk for z = ρeiθ
where k > 1 and M are constants then
M/ρk for z = ρeiθ
where k > 1 and M are constants then
![]()
Theorem 2. Let Γρ be a semicircular arc of radius ρ, in the upper half plane, centered at the
origin. See Fig. 6. If |f(z)|
![]() M/ρk for z = ρeiθ where k > 1 and M are constants then
M/ρk for z = ρeiθ where k > 1 and M are constants then
![]()
Theorem 3. Let Γρ be any circular arc of radius ρ centered at the origin. Let R(z) = P(z)/Q(z) be a rational function in which P(z) and Q(z) are polynomials and the degree of Q(z) is at least two greater than that of P(z). Then
![]()
Jordan’s lemma. Let Γρ be a semicircular arc of radius ρ, in the upper half plane, centered at the origin. See Fig. 6. Let R(z) = P(z)/Q(z) be a rational function in which P(z) and Q(z) are polynomials and the degree of Q(z) is at least one greater than that of P(z). Then
![]()
Leibnitz’s rule for differentiation under the integral sign. A method sometimes useful for evaluating integrals utilizes Leibnitz’s rule for differentiation under the integral sign. The rule states that
![]()
The rule is valid if a and b are constants, α is a real parameter such that α1
![]() α
α
![]() α2 where α1 and
α1 are constants, and f(x, α) is continuous and has a continuous partial derivative with respect to
α for a
α2 where α1 and
α1 are constants, and f(x, α) is continuous and has a continuous partial derivative with respect to
α for a
![]() x
x
![]() b, α1
b, α1
![]() α
α
![]() α2. It can be extended to cases where the limits a and b are infinite or
dependent on α.
α2. It can be extended to cases where the limits a and b are infinite or
dependent on α.
Residue theorem used to sum series. . The residue theorem can often be used to sum various types of series. Let us denote an infinite series such as, for example,
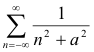
by the notation
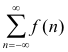
The following results are valid under very mild restrictions on f(z) which are usually satisfied whenever the series converge. Note that we replace n by the complex number z in the formula, viewing f(z) as complex.
![]()
![]()
![]()
![]()
Example. Evaluate
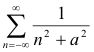
where a > 0.
Solution. Let
![]()
which has simple poles at z = ±ai.
The residue of
![]()
at z = ai is
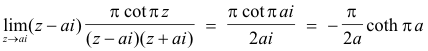
Similarly the residue at z = -ai is
![]()
The sum of the two residues is then
![]()
Consequently,
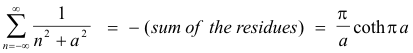
References
Spiegel. Complex Variables (Schaum)
Wylie. Advanced Engineering Mathematics
Hauser. Complex Variables with Physical Applications.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life