Prove: Let a function f(z) be analytic in a simply-connected region R and let C be a closed (not necessarily simple) curve in R. Then

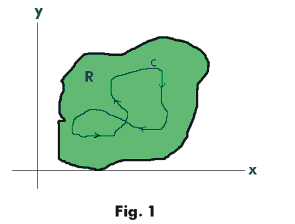
See Fig. 1.

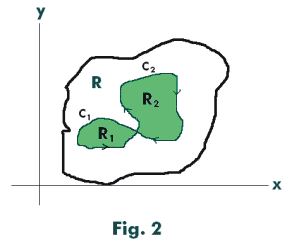
Proof. Suppose the curve is curve C shown in Fig. 1. Then C can be viewed as the boundary of two simply-connected region R₁ and R₂ shown in Fig. 2. Denote the two segments of C by C₁ and C₂. Applying Cauchy’s theorem we get

Thus