Prove. Let a function f(z) be analytic with a continuous derivative f '(z) within and on the boundary of a region R, either simply or multiply-connected, and let C be the entire boundary of R. Then

Proof. We first prove the theorem for a simply-connected region. Let the region R be simply-connected. Let f(z) = u(x, y) + i v(x, y). Then the integral around the boundary C is given by

Since f(z) is analytic with a continuous derivative in R and on the boundary C it follows that the conditions for Green’s theorem are met. Applying Green’s theorem to the two integrals in the right member we get

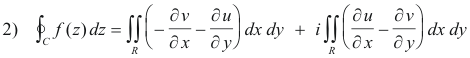
Because f(z) is analytic the Cauchy-Riemann equations

are satisfied and we see that both integrands in the right member of 2) are zero. Thus

Note. We have given the proof with the added condition that f '(z) be continuous in R but a proof can be given without this condition. See Spiegel. Complex Variables. (Schaum) Chap. 4.

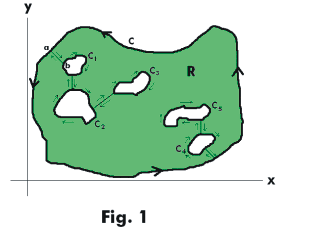
Proof for multiply-connected regions: Consider the multiply-connected region shown in Fig. 1 where cross-cuts have been constructed connecting the interior and exterior boundaries thus transforming the multiply-connected region into a simply-connected one where Cauchy’s theorem for simply-connected regions applies. We let the curve C of the theorem be the boundary of the simply-connected region shown in Fig. 1. The theorem states that

The total amount of curve traversed is equal to the boundaries C, C₁, C₂, C₃, C₄ and C₅ plus all the cross-cuts traversed. However, each cross-cut is traversed in opposite directions and the line integrals on the cross-cuts cancel each other out so the net amount of curve traversed that counts in the total is simply the boundaries C, C₁, C₂, C₃, C₄ and C₅ . And this is what Cauchy’s theorem of multiply-connected regions states.

Reference.

  Spiegel. Complex Variables. (Schaum) Chap. 4.