Example. Let u = e^-x(x sin y - y cos y)

(a) Prove u = e^-x(x sin y - y cos y) is analytic

(b) Find the conjugate harmonic function of u i.e. find a function v such that f(z) = u + iv is analytic

(c) Find f(z)

(a)     Prove u = e^-x(x sin y - y cos y) is analytic

            ∂u/∂x = (e^-x)(sin y) + (-e^-x)(x sin y - y cos y) = e^-x sin y - xe^-x sin y + ye^-x cos y

1)        ∂²u/∂x² = ∂(e^-x sin y - xe^-x sin y + ye^-x cos y)/∂x = -2e^-x sin y + xe^-x sin y - ye^-x cos y

            ∂u/∂y = e^-x (x cos y + y sin y - cos y) = xe^-x cos y + ye^-x sin y - e^-x cos y

2)        ∂²u/∂y² = ∂(xe^-x cos y + ye^-x sin y - e^-x cos y)/∂y = -xe^-x sin y + 2e^-x sin y + ye^-x cos y

Adding 1) and 2) gives ∂²u/∂x² + ∂²u/∂y² = 0 . Thus u is harmonic.

(b)    Find the conjugate harmonic function of u

From the Cauchy-Riemann equations we get

3)        ∂v/∂y = ∂u/∂x = e^-x sin y - xe^-x sin y + ye^-x cos y

4)        ∂v/∂x = - ∂u/∂y = e^-x cos y - xe^-x cos y - ye^-x sin y

We now integrate 3) with respect to y, keeping x constant:

5)        v = - e^-x cos y + xe^-x cos y + e^-x(y sin y + cos y) + F(x)

                        = ye^-x sin y + xe^-x cos y + F(x)

where F(x) is an arbitrary real function of x.

We now substitute 5) into 4), taking ∂v/∂x of 5)

            -ye^-x sin y - xe^-x cos y + e^-x cos y + F'(x) = e^-x cos y - xe^-x cos y - ye^-x sin y

or

            F'(x) = 0 .

Thus F(x) = c, a constant.

Substituting F(x) = c into 5) we get

            v = e^-x(y sin y + x cos y) + c

(c)      Find f(z)

To find f(z) we employ the following theorem:

Theorem 1. f(z) = u(z, 0) + i v(z, 0)

Derivation.

            f(z) = f(x+ iy) = u(x, y) + i v(x, y)

Putting y = 0, one obtains       f(x) = u(x, 0) + i v(x, 0)

Replacing x by z, we get        f(z) = u(z, 0) + i v(z, 0)

Solution. Applying Theorem 1 we get

u(z, 0) = 0

v(z, 0) = ze^-z

f(z) = u(z, 0) + i v(z, 0) = ze^-z,

apart from an arbitrary additive constant.

If only u (or v) is known another procedure can be used that employs the following theorem:

Theorem 2. If f(z) = u(x, y) + i v(x, y)

            f(z) = 2u(z/2, -iz/2) + constant 

and

            f(z) = 2i v(z/2, -iz/2) + constant

Alternative method for finding f(z) and the conjugate harmonic function. An alternative method for finding the conjugate harmonic function employs the following theorem:

Theorem 3. Let u₁ = ∂u/∂x and u₂ = ∂u/∂y. Then

            f '(z) = u₁(z, 0) - i u₂(z, 0)

Derivation. We have already shown that

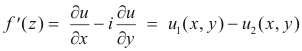
Putting y = 0, we get              f '(x) = u₁(x, 0) - i u₂(x, 0)

Then replacing x by z we obtain         f '(z) = u₁(z, 0) - i u₂(z, 0)

Solution. Since u = e^-x(x sin y - y cos y) , we have

            u₁(x, y) = ∂u/∂x = e^-x sin y - xe^-x sin y + ye^-x cos y

            u₂(x, y) = ∂u/∂y = xe^-x cos y + ye^-x sin y - e^-x cos y

Applying Theorem 3 we get

            f '(z) = u₁(z, 0) - i u₂(z, 0) = 0 - i(ze^-z - e^-z) = - i(ze^-z - e^-z)

Integrating with respect to z we obtain, except for a constant,

            f(z) = i ze^-z

If one then expands the right side in terms of x and y, one obtains

            f(z) = e^-x(x sin y - y cos y) + i e^-x(y sin y + x cos y)

giving

            v = e^-x(y sin y + x cos y)

Source: Spiegel. Complex Variables (Schaum). p. 73, 74, 85. Prob. 7, 8, 40, 101