Complex differentiation. Cauchy-Riemann equations. Analytic functions. Harmonic functions. Indeterminate forms. L’Hopital’s rule. Orthogonal trajectories. Curves. Elementary functions.
Derivatives of functions of a complex variable. The formal definition of the derivative of a function of a complex variable is exactly the same as for a real variable. Let f(z) be single-valued in some region R of the z-plane. Then the derivative of f(z) at a point z in R is defined as
![]()
provided the limit exists (and a limit is only regarded to exist if the same limit is reached regardless of the manner in which Δz → 0).
Necessary and sufficient conditions for the derivative of a function of a complex variable to exist. Let
w = f(z) = u(x, y) + iv(x, y)
be a function defined in the neighborhood of some point z0 of the z-plane. A necessary and sufficient condition for the derivative f '(z) to exist at point z0 is that u and v satisfy the conditions
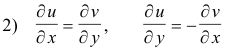
at the point. Also, it is required that the partial derivatives be continuous in the neighborhood of z0.
The equations 2) are called the Cauchy-Riemann equations.
With such severe conditions that must be met in order for a derivative to exist the reader must surely surmise that only relatively few functions have derivatives and wonder of how much use the concept of the derivative of a complex variable is. In fact, many functions do have derivatives and those functions that do are of great importance in applications.
Theorem 1. If the derivative f '(z) exists it is given by
![]()
Def. Analytic function. A function f(z) is said to be analytic at a point z0 if there exists some ε-spherical neighborhood of z0 at all points of which f '(z) exists. A function which is analytic at every point of a region R is said to be analytic in R.
If a function is analytic at a point then it can be expanded as a Taylor series
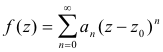
in the neighborhood of the point. And if a function can be expanded as a Taylor series in the vicinity of a point it is necessarily analytic at the point. Thus the property of a function having a derivative at a point and the property it being expandable as a Taylor series at the point imply each other. Some authors define analyticity at a point as the property of being expandable as a Taylor series at the point.
A function is sometimes said to be analytic in a region R if it is continuous in R and has a derivative at all except at most a finite number of points of R. If a function is differentiable at all points of R, it is a regular function, or a regular analytic function, or a holomorphic function in R.
Def. Singular point of an analytic function. A point at which an analytic function f(z) is not analytic is called a singular point or singularity of the function. A point at which a function is analytic is called a regular point.
Theorem 2. A necessary and sufficient condition that a single-valued function
w = f(z) = u(x, y) + iv(x, y)
be analytic in a region R is that the four partial derivatives ux, uy, vx, vy are continuous in R and that the Cauchy-Riemann equations
![]()
are satisfied in R.
Def. Harmonic function. A function Φ which satisfies Laplace’s equation
![]()
Theorem 3. Both the real part u and the imaginary part v of an analytic function
f(z) = u(x, y) + iv(x, y)
satisfy Laplace’s equation i.e.
![]()
providing the second partial derivatives exist and are continuous.
Thus both u and v are harmonic functions. They are called conjugate harmonic functions. Given one we can find the other (within an arbitrary additive constant) by integrating, using the Cauchy-Riemann equations. See Example
Theorem 4. Let u(x, y) be harmonic in some region R. Then there exists a function v(x, y) such that f(z) = u(x, y) + iv(x, y) is analytic in R.
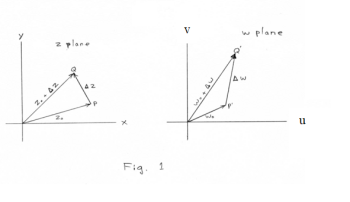
Geometric interpretation of the derivative. In the case of functions of a real variable the geometric (graphic) interpretation of the derivative as the slope of a curve is of great help in understanding the derivative and in using it in applications. What is the geometric interpretation of the derivative of a function of a complex variable? The derivative f '(z) of a function w = f(z) is given by
![]()
See Fig. 1. In the figure z0 is imaged into w0 and Δz is imaged into Δw. The problem thus reduces to that of giving a geometric interpretation to the quotient Δw/Δz of the two complex quantities Δw and Δz. What intuitive concept does this provide? I don’t know of one.
Theorem 5. If f(z) is analytic in a region R, then derivatives of all orders f '(z), f ''(z), f '''(z), ... exist in R.
From this theorem it follows that if a function is analytic in a region, it can be expanded as a Taylor series at points within the region.
Indeterminate forms, L’Hopital’s rule. Limits involving indeterminate forms 0/0, ∞/∞, 0∙∞, ∞0, 00, 1∞ and ∞ - ∞ can often be evaluated by L’Hopital’s rule or appropriate modifications of it. Let f(z) and g(z) be analytic in a region. If the fraction f(z)/g(z) assumes one of the indeterminate forms 0/0 or ∞/∞ when z = a, then
![]()
A similar statement holds if the indeterminate form arises when z becomes infinite instead of when z = a.
If f '(z)/g'(z) also assumes an indeterminate form of the type 0/0 or ∞/∞, the rule can be applied likewise to it. The process can, in fact, be repeated as many times as necessary to yield a fraction f(n)(a) / g(n)(a) which is not indeterminate.
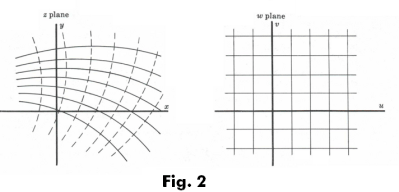
Def. Orthogonal trajectories. Two families of curves with the property that each member of either family cuts each family of the other family at right angles.
Orthogonal families. If
w = f(z) = u(x, y) + iv(x, y)
is an analytic function, the curves of the family u(x, y) = c are the orthogonal trajectories of the curves of the family v(x, y) = k. In the z plane of Fig. 2 the curves of the family u(x, y) = c are shown as solid lines plotted for different values of the constant c and the curves of the family v(x, y) = k are shown as dashed lines plotted for different values of the constant k. Thus we see that the families u(x, y) = c and v(x, y) = k form two orthogonal families. The corresponding image curves in the w plane consisting of lines parallel to the u and v axes also form orthogonal families.
Equation of a continuous curve in the z plane. How does one represent a curve in the z plane? The x and y in z = x + iy can be given by the parametric system
x = x(t)
y = y(t)
where x(t) and y(t) are real functions of the real variable t,
assumed to be continuous in the interval t1
![]() t
t
![]() t2 . z is then
given by
t2 . z is then
given by
![]()
which defines a continuous curve or arc extending from point a = z(t1) to b = z(t2). See Fig. 3.
If t1 ≠ t2 while z(t1) = z(t2), i.e. a = b, the end points coincide and the curve is said to be closed. A closed curve that does not intersect itself anywhere is called a simple closed curve. The curve in Fig. 4 is a simple closed curve while the curve in Fig. 5 is not.
Def. Smooth curve or arc. A curve defined by 3) is called
smooth if x(t) and y(t) [and thus z(t)] have continuous
derivatives in the interval t1
![]() t
t
![]() t2 .
t2 .
Def. Piecewise or sectionally smooth curve. A curve that is composed of a finite number of smooth arcs.
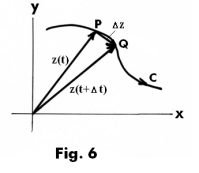
We can consider z(t) in 3) as a position vector whose terminal point traces out a curve C in a
particular sense or direction as t increases from t1 to t2. Let z(t) and z(t + Δt) represent position
vectors of points P and Q respectively. Then
![]()
is a vector in the direction Δz. See Fig. 6. If
![]()
exists, the limit is a vector in direction of the tangent to C at point P and is given by
![]()
If t represents time, then dz/dt represents the velocity with which the terminal point traces out the curve. Similarly, d2z/dt2 represents its acceleration along the curve. Spiegel. Complex Variables. p. 68-69
The elementary functions. We shall now give a definition to a class of functions called elementary functions. To do this we shall label another collection of functions the simple elementary functions. Elementary functions are built up from the simple elementary functions.
-----------------------------------------------------------------------------------------------------------------
The Simple Elementary Functions: c, z, za, ez, az, ln z, logb z, sin z, cos z, tan z, ..., sin-1 z, cos-1 z, tan-1 z, ... , sinh z, cosh z, tanh z, ..., sinh-1 z, cosh-1 z, tanh-1 z, ... where c and a are complex constants, b is real, and z is a complex variable.
-----------------------------------------------------------------------------------------------------------------
The simple elementary functions include the familiar exponential, logarithmic, trigonometric and hyperbolic functions plus the variable z and the constant c. Utilizing the term “simple elementary function” we now define the term “elementary function”.
Def. Elementary function. An elementary function is any function that can be built from the simple elementary functions by the four arithmetic operations of addition, subtraction, multiplication and division and the operation of taking a function of a function, each of these operations being performed a finite number of times.
Any complex expression built by these rules from the simple elementary functions is an elementary function. For example
![]()
are both elementary functions. So is
![]()
since it is obtained from the polynomial u = 1- x2 by the operation
![]() , and subsequently by
the operation ln v.
, and subsequently by
the operation ln v.
Note. All of the simple elementary functions themselves also qualify as being elementary functions, from the wording of this definition. However, the concept of an elementary function is that of a complex function built up of simple elementary functions. The simple elementary functions are often referred to as “the elementary functions”, a cause for some confusion.
Theorem 6. Every elementary function is analytic and can be expanded in a Taylor series at every point in its domain of definition.
References
Mathematics, Its Content, Methods and Meaning
James and James. Mathematics Dictionary
Spiegel. Complex Variables (Schaum)
Wylie. Advanced Engineering Mathematics