Website owner:  James Miller

Prove: Let F(t) be a continuous, piecewise regular function of exponential order. Furthermore, let F '(t) be sectionally continuous. Then if L[F (t)] = f(s), the Laplace transform of F '(t) is given by the formula

            L[F '(t)] = sf (s) - F(0)

Proof. We will first prove this theorem for the case when F '(t) is continuous (as opposed to sectionally continuous).

Case 1. F '(t) is continuous.

We shall now integrate the rightmost member by parts using the formula

 where u = e^-st, dv = F ' (t) dt, v = F(t), du = -se^-st dt

Now because F(t) is of exponential order

for s > α₀, the abscissa of convergence of F(h). Thus 2) becomes

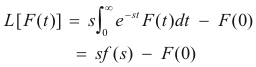
Case 2. F '(t) contains one discontinuity. Assume that F '(t) has a discontinuity at t = t₀. See Fig. 1. Then

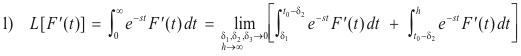
Integrating the two integrals by parts gives

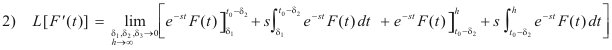
We now note that in the limit the sum of the two integrals is

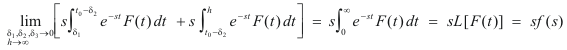
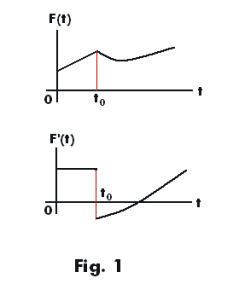
The first evaluated portion gives

and the second gives simply

because, since F(t) is of exponential order, the contribution from the upper limit is zero. Now F(t) was assumed to be continuous and hence at t = t₀ its right- and left-hand limits must be equal. Thus the terms

cancel, giving as the final result

Website owner:  James Miller