Laplace transform. Dirichlet conditions. Sectionally continuous (or piecewise continuous) function. Function of exponential order. Piecewise regular function. Inverse Laplace transform. Properties of Laplace transforms. Initial and final-value theorems.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Use of Laplace transforms. Laplace transforms find wide use in solving linear differential equations with constant coefficients, linear constant-coefficient integro-differential equations, convolution type integral equations, difference equations, differential-difference equations and many boundary value problems.

Dirichlet conditions. The following conditions on a function defined over some interval [a, b] are called the Dirichlet conditions:

(a) it is continuous except for a finite number of discontinuities

(b) it has only a finite number of maxima and minima.

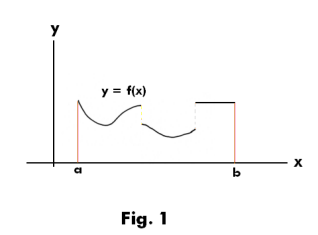
Def. Sectionally continuous (or piecewise continuous) function. A function f (x) is said to be sectionally continuous (or piecewise continuous) on an interval a x b if the interval can be subdivided into a finite number of intervals in each of which the function is continuous and has finite right and left hand limits. See Fig. 1. The requirement that a function be sectionally continuous on some interval [a, b] is equivalent to the requirement that it meet the Dirichlet conditions on the interval.

Def. Laplace transform. Let F(t) be a real-valued function of the real variable t defined on the positive portion of the real axis, t 0. Then the Laplace transform of F(t), denoted by L [F(t)], is defined as

where in general s is real, but for some considerations needs to be viewed as complex.

For the Laplace transform to exist, the improper integral

must converge for some range of values of s. A sufficient condition for this integral to converge is that F(t) be of exponential order.

Note. When talking about the Laplace transform of functions it is tacitly assumed that the function is defined only on the positive portion of the real axis, t 0, and is undefined or zero in the negative portion of the axis.

Def. Function of exponential order. A function F(t) is said to be of exponential order if there exist real constants α, M, and T such that

2) e^-αt|F(t)| < M for all t > T

or, equivalently,

3) |F(t)| < e^αt M for all t > T

If condition 3) holds for α = α₁, then it will obviously hold for all α’s greater than α₁. The greatest lower bound α₀ of the set of all α’s for which 3) is satisfied is called the abscissa of convergence of F(t).

From 3) one can see that if a function is of exponential order its absolute value need not remain bounded as t → ∞, but it must not increase more rapidly than some constant multiple of a simple exponential function of t.

Def. Piecewise regular function. A piecewise regular function is a function defined on the positive real axis, t 0, that is sectionally continuous in every finite subinterval of that axis (every finite subinterval of the positive real axis 0 t ).

Theorem 1. Let F(t) is a piecewise regular function defined on the positive real axis, t 0. Let F(x) be of exponential order. Then its Laplace transform f(s) exists for all s > α₀, where α₀ is the abscissa of convergence of f(t).

Inverse Laplace transform. Let F(t) is a piecewise regular function defined on the positive real axis, t 0. Let F(x) be of exponential order. Then the Laplace transform

of F(t) exists in the half-plane of the complex variable s for which the real part of s is greater than the abscissa of convergence α₀ of F(t) i.e. R(s) > α₀. In addition, the inverse Laplace transformation L^-1[f(s)] also exists in this half-plane and is given by

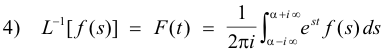
where α > α₀. This path of integration represents a path lying to the right of all of the singularities of f (s).

Formula 4) is referred to as the Complex inversion formula.

Proof of Complex inversion formula

Laplace transforms of some elementary functions

	F(t)	L[F(t)] = f(s)
1.	1
2.	t
3.
4.
5.	sin at
6.	cos at
7.	sinh at
8.	cosh at

Proofs

Important properties of Laplace transforms

1. Linearity property. Let c₁ and c₂ be any constants and F₁(t) and F₂(t) be functions with Laplace transforms f₁(s) and f₂(s) respectively. Then

5) L[c₁ F₁(t) + c₂ F₂(t)] = c₁ L [F₁(t)] + c₂ L [F₂(t)] = c₁ f₁(s) + c₂ f₂(s)

Proof

Example.

L[2t³ - 4 cos 3t + 2e^-t] = 2L[t³] - 4L[cos 3t] + 2L[e^-t]

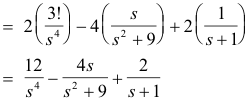
We thus see that a Laplace transform effects a linear transformation. A Laplace transform represents what is called a linear operator.

2. First translation (or shifting) property. If L[F(t)] = f(s) then

6) L[e^atF(t)] = f(s - a)

Proof

Problem. Find L [e^{2 t}sin 3t].

Solution. Let F(t) = sin 3t. Then

and

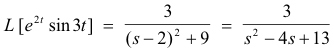
We note that the function f(s - a) is the function f(s) shifted to the right by a distance a.

3. Second translation (or shifting) property. Let L[F(t)] = f(s) and

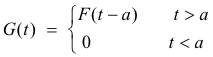
Then

7) L[G(t)] = e^-asf(s)

Proof

Problem. Find L[G(t)] where

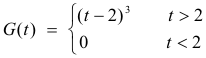
Solution. Since

4. Change of scale property. If L[F(t)] = f(s) then

Proof

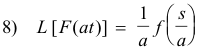
Problem. Find L[sin 4t)].

Solution. Since

we obtain

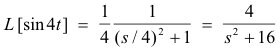
5. Laplace transform of derivatives.

Theorem 2. Let F(t) be a continuous, piecewise regular function of exponential order. Furthermore, let F '(t) be sectionally continuous. Then if L[F (t)] = f(s), the Laplace transform of F '(t) is given by the formula

9) L[F '(t)] = sf (s) - F(0)

Proof

If F(t) is discontinuous at t = 0 but the limit as t approaches zero from the right

exists, then the formula is

10) L[F '(t)] = sf (s) - F(0⁺)

Note. Note that in the case where F(t) is continuous at t = 0, L[F '(t)] is also given by

L[F '(t)] = sf (s) - F(0⁺)

since in this case F(0) = F(0⁺). Thus 10) applies to both cases.

If F (t) is discontinuous at t = a, then

11) L[F '(t)] = sf (s) - F(0) - e^-as [F(a⁺) - F(a^-)]

where the quantity F(a⁺) - F(a^-) is called the jump at the discontinuity t = a. If there is more than one discontinuity, appropriate modifications can be made.

Theorem 3. Let F (t) and F '(t) be continuous, piecewise regular functions of exponential order. Furthermore, let F ''(t) be sectionally continuous. Then if L[F (t)] = f(s), the Laplace transform of F ''(t) is given by

12) L[F '' (t)] = s²f (s) - sF(0) - F '(0)

If F (t) is discontinuous at t = 0, this formula becomes

13) L[F ''(t)] = s²f (s) - sF(0⁺) - F '(0⁺)

If other discontinuities exist, modifications can be made.

Theorem 4. Let F(t), F '(t), .... , F ^{(n -1)}(t) be continuous, piecewise regular functions of exponential order. Furthermore, let F ⁽ⁿ⁾ (t) be sectionally continuous. Then if L[F(t)] = f(s), the Laplace transform of F ⁽ⁿ⁾ (t) is given by

14) L[F ⁽ⁿ⁾ (t) ] = sⁿf (s) - s ^{n -1}F(0) - s ^{n -2}F '(0) - - sF ^{(n - 2)}(0) - F ^{(n - 1)}(0)

If F(t) is discontinuous at t = 0, this formula becomes

15) L[F ⁽ⁿ⁾ (t) ] = sⁿf (s) - s ^{n -1}F(0⁺) - s ^{n -2}F '(0⁺) - - sF ^{(n - 2)}(0⁺) - F ^{(n - 1)}(0⁺)

Problem. Let F(t) = cos 4t. Find L[F '(t)] i.e. L[- 4 sin 4t]

Solution. Since

we have

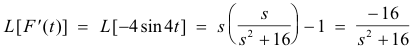
6. Laplace transform of integrals. If L[F(t)] = f(s), then

Proof

Example. Since

we have

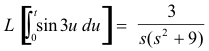
7. Multiplication by tⁿ. If L[F(t)] = f(s), then

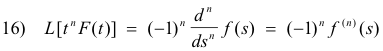
Problem. Find L[t²e^2t].

Solution. Since

we have

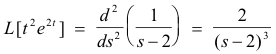
8. Division by t. If L[F(t)] = f(s), then

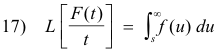
provided

exists.

Example. Since

we have

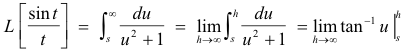
9. Periodic functions. Let F(t) have the period T so that F(t + T) = F(t). See Fig. 2. Then

Proof

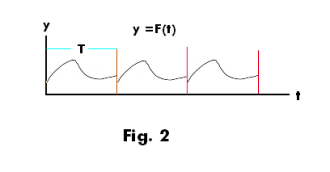
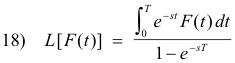
10. Behavior of f(s) as s → ∞. If L[F(t)] = f(s), then

11. Initial -value theorem. Let L[F(t)] = f(s) and let F(t) and F '(t) both be piecewise regular and of exponential order. Then

Proof

12. Final -value theorem. Let L[F(t)] = f(s). If F(t) and F '(t) are both piecewise regular and of exponential order, and if the abscissa of convergence of F '(t) is negative, then

provided these limits exist.

Proof

Notation. If, for two functions p(t) and q(t), , we say that for values of t near t = a, p(t) is approximately equal to q(t) and write p(t) ~ q(t) as t → a.

13. Generalization of initial -value theorem. Let L[F(t)] = f(s) and L[G(t)] = g(s). Then if F(t) ~ G(t) as t → 0, then f(s) ~ g(s) as s → ∞.

14. Generalization of final -value theorem. Let L[F(t)] = f(s) and L[G(t)] = g(s). Then if F(t) ~ G(t) as t → ∞, then f(s) ~ g(s) as s → 0.

Theorem 2. Let L[F(t)] = f(s). Then

provided the integral is convergent.

Proof. By definition

Taking the limit of both sides as s → 0, we get

References

Murray R. Spiegel. Laplace Transforms. (Schaum)

C. R. Wylie, Jr. Advanced Engineering Mathematics.