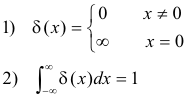
Website owner: James Miller
Theorems involving Impulse function. Complex Fourier series representation and Fourier transform of a train of rectangular pulses of width d with period T.
Impulse function (also called Delta function). The impulse function δ(x) (which is not really a function in the usual sense of the word) has the following two properties:
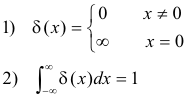
It can be defined as:
![]()
The τ-1II(x/τ) product represents a rectangle function of height 1/τ and base τ and with unit area. As τ approaches zero a sequence of unit-area pulses of ever-increasing height are generated. The limit of the integral is, of course, equal to 1.
Theorems involving the impulse function
Theorem 1. Given any function f(x), the following holds:
![]()
which is deemed to mean
![]()
where the τ-1II(x/τ) product represents a rectangle, centered at the origin, of height 1/τ, base τ, and with unit area. As τ →0, f(x) → f(0) and the limit is equal to
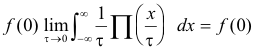
Theorem 2. The Fourier transform of δ(x) is given by (using the definition of the Fourier transform and Theorem 1):
![]()
Thus the Fourier transform of the unit impulse function is unity.
Theorem 3
![]()
where ω = 2πs.
Derivation. Applying the inverse Fourier transform to 4) gives
![]()
Theorem 4
![]()
Derivation.
![]()
Because δ(x) is an even function, the sin integral is equal to zero and
![]()
Thus we have
![]()
___________________________________
Note that the quantity δ(t-t0) represents a unit impulse at t = t0.
Theorem 5
![]()
Derivation. Let τ = t - t0. Then t = τ + t0 and dt = dτ.
![]()
Then by Theorem 1
![]()
___________________________________
Theorem 6. Given function f(t)
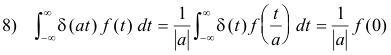
Derivation. Let τ = at. Then t = τ/a, dt = (1/a) dτ.
Case 1. a > 0.
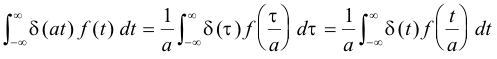
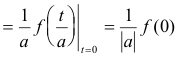
Case 2. a < 0.
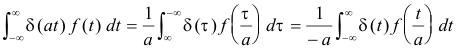
![]()
___________________________________
Theorem 7. Let g(t) be continuous at t = t0 and a < b. Then
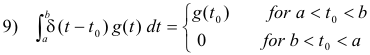
Theorem 8. Let a < b. Then
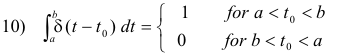
Theorem 9. Let f(t) be continuous at t = t0. Then
1) f(t) δ(t) = f(0) δ(t)
2) t δ(t) = 0
3) δ(at) = [1/|a|] δ(t)
4) δ(-t) = δ(t)
Theorem 10. The Fourier transform of a constant function
f(t) = a
expressed as a function of the impulse function is
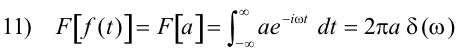
Theorem 11. Let ω0 be a real constant and let F(ω) be the Fourier transform of f(t) i.e. F(ω) = F[f(t)]. Then
![]()
Derivation.
![]()
Theorem 12. Let F(ω) be the Fourier transform of f(t). Then the Fourier transform of f(t) cos ω0t is given by
![]()
Derivation. Using the identity
![]()
and Theorem 11 we get
![]()
![]()
Theorem 13. The Fourier transform of
![]()
expressed in terms of the impulse function is
![]()
Derivation. From Theorem 10 we have
F[f(t) =1] = 2π δ(ω)
and from Theorem 11 we have
![]()
Thus
![]()
Fourier transforms of cos ω0t and sin ω0t
Theorem 14. The Fourier transforms of cos ω0t and sin ω0t expressed in terms of the impulse function are
15) F[cos ω0t] = π δ(ω - ω0) + π δ(ω + ω0)
16) F[sin ω0t] = -iπ δ(ω - ω0) + iπ δ(ω + ω0)
Derivation. The formulas follow from the use of Theorem 10 and Theorem 12.
Fig. 1 (a) shows the function f(t) = cos ω0t and Fig. 1 (b) shows its Fourier transform.
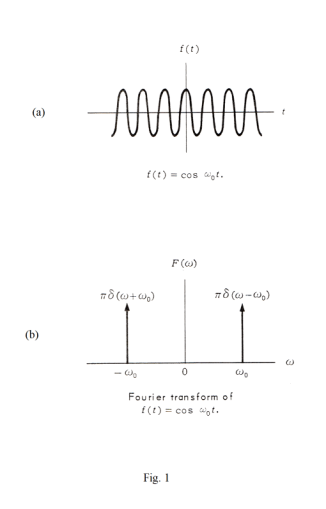
Fourier transform of a unit step function. The Fourier transform of a unit step function u(t) defined by
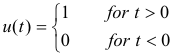
is
![]()
If the Fourier transform is written as
F(ω) = R(ω) + i X(ω)
then
R(ω) = π δ(ω)
X(ω) = -1/ω
See Fig. 2. It can be seen that it contains an impulse at ω = 0.
The Fourier transform of a periodic function. A periodic function f(t) with a period T can be expressed as
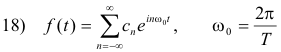
Theorem 15. The Fourier transform of the periodic function f(t) with a period T
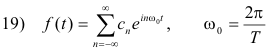
is given by
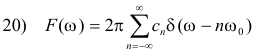
This means that the Fourier transform of a periodic function consists of the sum of a sequence of equidistant impulses located at the harmonic frequencies of the function.
Derivation. Taking the Fourier Transform of both sides of 19) gives
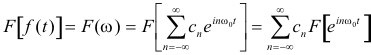
From Theorem 13
![]()
so the Fourier transform of f(t) is
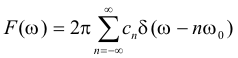
___________________________________
Fourier transform of a unit impulse train. The unit impulse train function is defined by
δT(t) = ..... + δ(t + 3T) + δ(t + 2T) + δ(t + T) + δ(t) + δ(t - T) + δ(t - 2T) + δ(t - 3T) + .....
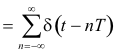
and consists of the sum of an infinite sequence of equally spaced unit impulses.
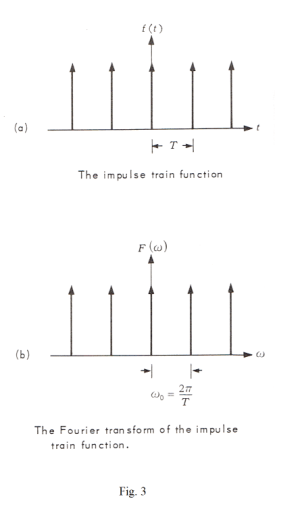
Theorem 16. The Fourier transform of the unit impulse train function is
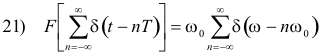
Thus the Fourier transform of a unit impulse train is a similar impulse train. See Fig. 3. Consequently, we can say that the impulse train function is its own transform.
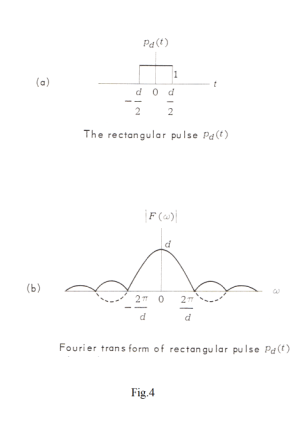
Fourier transform of a rectangular pulse. Let Pd(t) denote the function
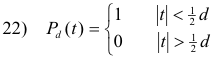
consisting of a single pulse of unit height and width d, centered at the origin, as shown in Fig. 4(a).
Theorem 17. The Fourier transform of the function Pd(t) is given by
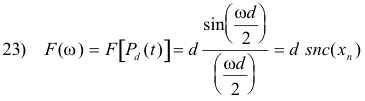
where snc (xn) = (sin xn)/xn is one variation of the sinc function and
xn = ωd/2
See Fig. 4(b).
Derivation.
![]()
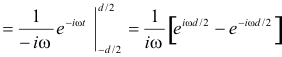
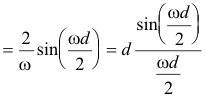 ___________________________________
___________________________________
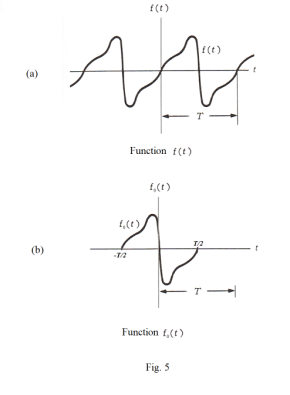
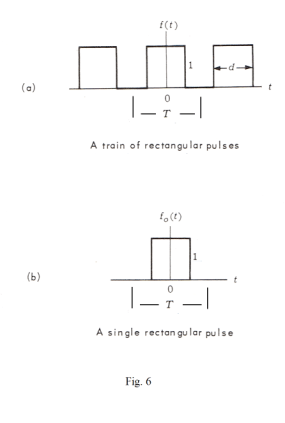
Complex coefficients cn of the Fourier series expansion of a periodic function. Let f(t) be an arbitrary periodic function with period T such as the one shown in Fig 5 (a). Let f0(t) be that function obtained by translating the basic cycle of f(t) so as to center it over the origin and retaining only the basic cycle as shown in Fig. 4 (b) i.e.
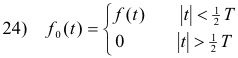
Theorem 18. The complex coefficients cn of the Fourier series expansion of the periodic function f(t) are equal to the values of the Fourier transform F0(ω) of the function f0(t) at ω = nω0 = n2π/T i.e.
![]()
Proof. The periodic function f(t) with period T can be written as
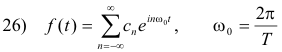
where
![]()
Now
![]()
Substituting nω0 for ω in 28) gives
![]()
Substituting 29) into 27) gives
![]()
___________________________________
Complex Fourier series representation of a train of rectangular pulses of width d with period T. Let f(t) be a train of rectangular pulses of width d with period T as shown in Fig. 6 (a). Let f0(t) be that function obtained by translating the basic cycle of f(t) so as to center it over the origin and retaining only the basic cycle as shown in Fig. 4 (b) i.e.
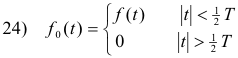
The complex Fourier series representation of f(t) is given by
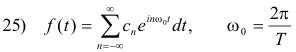
By Theorem 17 the Fourier transform of the function f0(t) is given by
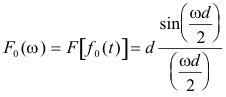
and by Theorem 18 the complex coefficients cn of f(t) are equal to the values of the Fourier transform F0(ω) of the function f0(t) at ω = nω0 = n2π/T i.e.
![]()
Thus the complex coefficients cn of f(t) are given by
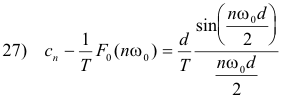
Fourier transform of a train of rectangular pulses of width d with period T. Let f(t) be a train of rectangular pulses of width d with period T as shown in Fig. 6 (a). The complex Fourier series representation of f(t) is given by
![]()
where the complex coefficients cn of f(t) are given by
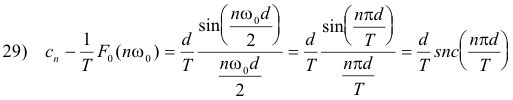
where snc x = (sin x)/x. It is a variation of the sinc function. It now follows from Theorem 15 that the Fourier transform of f(t) is given by
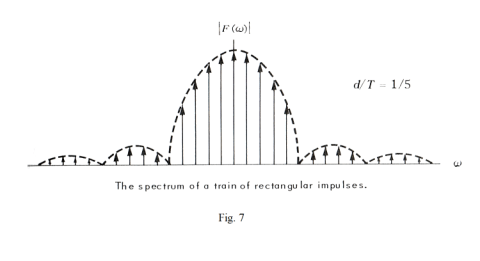
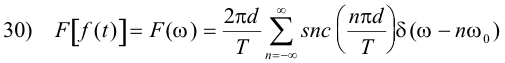
Equation 30) reveals that the Fourier transform of a function consisting of a train of rectangular pulses such as that shown in Fig. 6(a) consists of impulses located at ω = 0, ±ω0, ±2ω0, ±3ω0, ..... , etc. The strength of the impulse located at ω = nω0 is given by (2πd/T) snc (nπd/T). A spectrum is shown in Fig. 7 for a d/T = 1/5 case.
References
Hsu. Fourier Analysis
Bracewell. The Fourier Transform and Its Applications
James, James. Mathematics Dictionary
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life