Properties and Fourier transforms of even and odd functions. Hermitian function. Complex conjugates.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Def. Even function. A function f such that f(-x) = f(x) for all x in the domain of f.

Examples. x², cos x

Def. Odd function. A function f such that f(-x) = -f(x) for all x in the domain of f.

Examples. x³ and sin x since (-x)³ = -x³ and sin(-x) = - sin x

The concepts of evenness and oddness are defined for both real-valued and complex-valued functions of a real or complex variable. In the case of real-valued functions of a real variable, the graph of f(-x) is the graph obtained by reflecting the graph of f(x) about the y axis. The graph of an even function is symmetric with respect to the y-axis and the graph of an odd function is symmetric with respect to the origin (it is unchanged when reflected about both the x-axis and y-axis).

Theorem 1. Any function f(x) can be expressed uniquely as a sum of an even function E(x) and an odd function O(x)

f(x) = E(x) + O(x)

where

E(x) = ½[f(x) + f(-x)]

O(x) = ½[f(x) - f(-x)]

Proof

Properties of even and odd functions

Properties involving addition and subtraction

● The sum of two even functions is even, and any constant multiple of an even function is even.

● The sum of two odd functions is odd, and any constant multiple of an odd function is odd.

● The difference between two odd functions is odd.

● The difference between two even functions is even.

● The sum of an even and odd function is neither even nor odd, unless one of the functions is equal to zero over the given domain.

Properties involving multiplication and division

● The product of two even functions is an even function.

● The product of two odd functions is an even function.

● The product of an even function and an odd function is an odd function.

● The quotient of two even functions is an even function.

● The quotient of two odd functions is an even function.

● The quotient of an even function and an odd function is an odd function.

Calculus properties

● The derivative of an even function is odd.

● The derivative of an odd function is even.

● The integral of an odd function from -A to +A is zero (where A is finite, and the function has no vertical asymptotes between -A and A).

● The integral of an even function from -A to +A is twice the integral from 0 to +A (where A is finite, and the function has no vertical asymptotes between -A and A. This also holds true when A is infinite, but only if the integral converges).

Series properties

● The Maclaurin series of an even function includes only even powers.

● The Maclaurin series of an odd function includes only odd powers.

● The Fourier series of a periodic even function includes only cosine terms.

● The Fourier series of a periodic odd function includes only sine terms.

Algebraic properties

Any linear combination of even functions is even, and the even functions form a vector space over the reals. Similarly, any linear combination of odd functions is odd, and the odd functions also form a vector space over the reals. The vector space of all real-valued functions is the direct sum of the subspaces of even and odd functions. In other words, every function f(x) can be written uniquely as the sum of an even function and an odd function.

Sine - Cosine form of Fourier Transform. By definition, the Fourier transform of the function f (t) is F(ω) as given by the formula

Using the fact that for any real number x,

e^-ix= cos x - i sin x

1) becomes

Fourier transforms of even and odd functions

Let us consider the function

4) f (x) = e(x) + o(x)

where e(x) is an even function of x, o(x) is an odd function of x, and e(x) and o(x) are in general

complex. The Fourier cosine transform of e(x) is

and the Fourier sine transform of o(x) is

and the Fourier transform of f (x) = e(x) + o(x) is

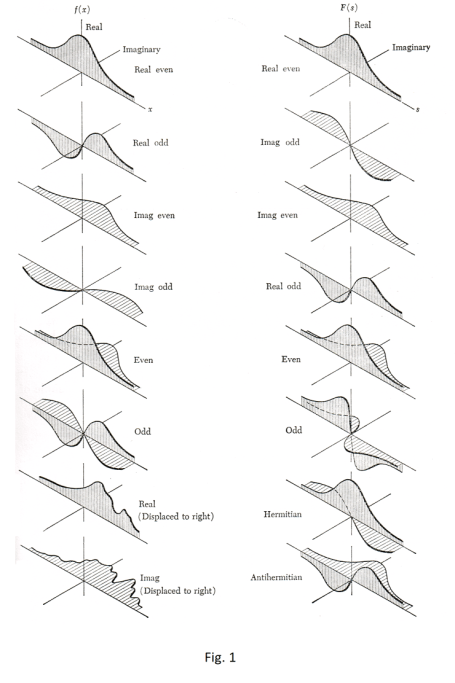
The function f (x) is a complex-valued function of a real variable x. This function can be depicted using a three-dimensional Cartesian coordinate system with one axis labeled “x”, another axis labeled “Real”, and a third axis labeled “Imaginary” as shown in Fig. 1. For each value x = x_i , f (x) = a_i + b_i i and the real and imaginary components of f (x) are plotted as a function of x. There are a number of possibilities for the function f (x). It can be real and even, real and odd, imaginary and even, imaginary and odd, complex and even, complex and odd, etc. Each of these possibilities gives rise to a characteristic Fourier transform as shown in the following table.

Function f (x) Fourier transform

_______________________________________________________________

Real and even Real and even

Real and odd Imaginary and odd

Imaginary and even Imaginary and even

Imaginary and odd Real and odd

Complex and even Complex and even

Complex and odd Complex and odd

Real and asymmetrical Complex and asymmetrical

Imaginary and asymmetrical Complex and asymmetrical

Real even and imaginary odd Real

Real odd and imaginary even Imaginary

Even Even

Odd Odd

These different transform results are depicted in Fig. 1 and are summarized in the following diagram:

Hermitian functions

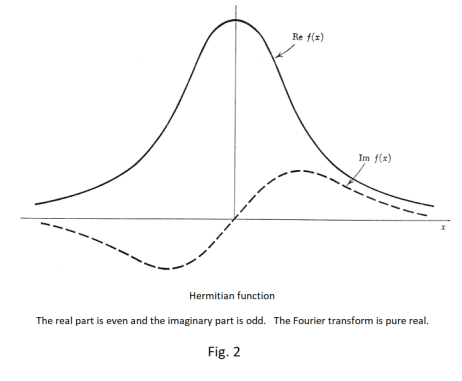
Def. Hermitian function. A function defined by the property f (x) = f *(-x), where the asterisk denotes the complex conjugate.

A property of a Hermitian function is that its real part is even and its imaginary part is odd. See Fig. 2.

Theorem 2. If a function has the property that f (x) = f *(-x) then its real part is even and its imaginary part is odd.

Proof. Let f (x) be written as the sum of an even and odd function:

f (x) = e(x) + o(x)

f (x) = E + O + iE + iO

where e(x) = E + iE and o(x) = O + iO

Then

f (-x) = E - O + iE - iO

and

f *(-x) = E - O - iE + iO

If we now require that f (x) = f *(-x) then necessarily O = 0 and E = 0. Thus f (x) = E + iO.

Complex conjugates. The Fourier transform of the complex conjugate of a function f (x) is F*(-s) i.e. it is the reflection of the conjugate of the transform. Special cases are as follows:

Function f (x) Fourier transform

_______________________________________________________________

real F(s)

imaginary -F(s)

even F*(s)

odd -F*(s)

References

Hsu. Fourier Analysis

Bracewell. The Fourier Transform and Its Applications

James, James. Mathematics Dictionary

Spiegal. Laplace Transforms. (Schaum) Chap. 6

Wikipedia