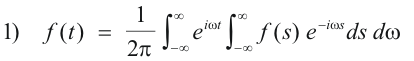
Prove. The following are equivalent forms of the Fourier integral:

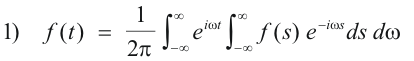
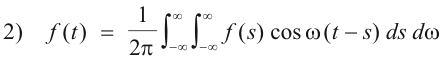
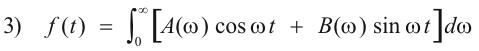
where

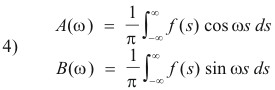
Proof.

Part 1. We shall first show that 2) is equivalent to 1). We can move the factor e^iωt in 1) into the inner integral since it doesn’t involve the variable s. Thus 1) becomes

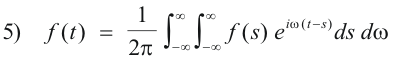
Now, using the general formula e^iθ = cos θ + i sinθ, we replace the factor e^iω(t-s) with its trigonometric equivalent to get

or, equivalently,

Now because f(t) is by hypothesis real, the imaginary part of 7) is zero. Thus 7) becomes

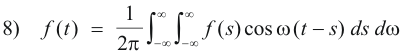
which is 2) above.

Part 2. We shall now show that 3) is equivalent to 2). First we note that because the integrand of 2) is an even function of ω, we need perform the ω-integration only between 0 and , provided we multiply the result by 2. Thus 2) is equivalent to

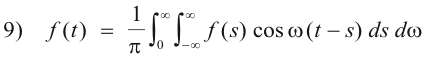
We now substitute 4) into 3) to obtain

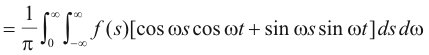
Now using the general formula from trigonometry

            cos (A - B) = cos A cos B + sin A sin B

we rewrite 10) as

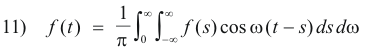
which is 9) and equivalent to 2).