Prove. If we substitute the Euler exponential equivalents

into the sine and cosine terms of the Fourier series

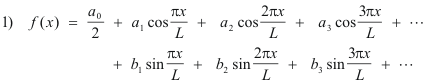
we obtain the Complex Fourier Series

where

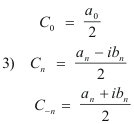
or, equivalently,

Proof. Substituting

into 1) we obtain

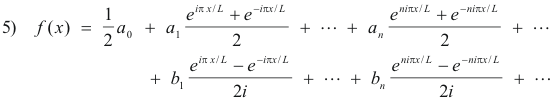
Since 1/i = -i, 21) becomes

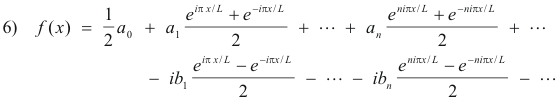
which becomes

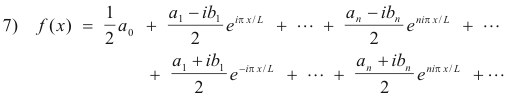
If we now define

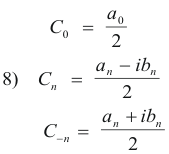
7) can be written as

or

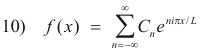
Now C₀, C_n and C_-n are given by

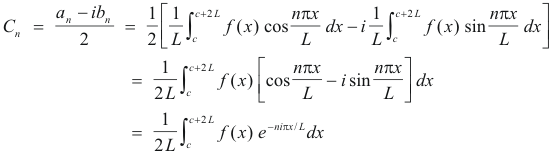
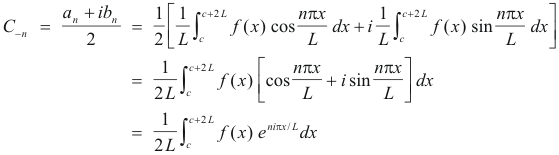
We see from the above formulas that whether the index n is positive, negative, or zero, C_n is given by the single formula