Prove: Let f(x) be an even function. Prove the coefficients in the Fourier series of f(x) are given by

Proof.

(a) For a function defined on the interval (-L, L) we have

Let us now make a change of variables in the first integral on the right side, letting x = -u. Noting, in regard to the limits, that u = L corresponds to x = -L and u = 0 corresponds to x = 0, we have

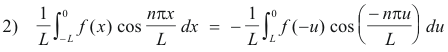
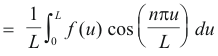
since f(-u) = f(u) and

Thus 1) becomes

since the two integrals on the right are identical except for the dummy argument of integration u in the first, which is immaterial.

(b) For a function defined on the interval (-L, L) we have

Again letting x = -u in the first integral on the right we get

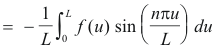
since f(-u) = f(u) and

Thus 4) becomes

since the two integrals are the same except for the dummy variable u.