Prove. The square of the length of a vector in Hilbert space is equal to the sum of the squares of its projections onto a complete system of mutually orthogonal directions. In other words, if

are a complete orthonormal system of functions in Hilbert space and if a function f is given by

then

Proof. Denote by r_n(x) the difference between f (x) and the sum of the first n terms of its series representation i.e.

Now the function r_n(x) is orthogonal to each of the functions . Let us show that it is orthogonal to, for example, the function , i.e., show that

We have

or

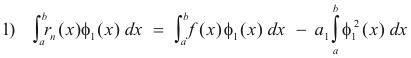
where we employ the fact that, because the functions are orthogonal to each other,

Now in 1)

and thus 1) becomes

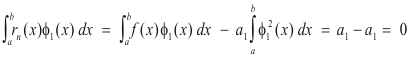
Hence, in the equation

the individual terms on the right side are all orthogonal to each other. Now, by the Pythagorean theorem, the square of the length of f (x) is equal to the sum of the square of the summands on the right side of 2), i.e.

Since the system of functions is normalized, we have

Now we are dealing with functions of a Hilbert space and a Hilbert space consists of those functions f for which the Legesgue integral of | f ² | exists. This means that as n approaches , the integral

converges and the quantity

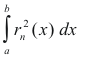
on the right side of 3) approaches zero. Thus formula 3) becomes

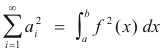
Source: Mathematics, Its Content, Methods and Meaning. Vol. 3, pp.243-244