Expansion by orthogonal systems of functions in Hilbert space. Complete orthogonal systems. Orthonormal systems. Generalized Fourier series, coefficients. Parseval�s identity.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Expansion by orthogonal systems of functions in Hilbert space. Complete orthogonal systems. Orthonormal systems. Generalized Fourier series, coefficients. Parseval’s identity.

Def. Orthogonal system. A system of functions

is called orthogonal if every function is orthogonal to every other function i.e. if

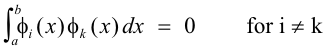
Examples of orthogonal systems.

1. The sequence of trigonometric functions

1, cos x, sin x, cos 2x, sin 2x, .... , cos nx, sin nx, .....

on the interval (-π, π). This system is one of the first and most important examples of orthogonal systems, appearing in works of Euler, D. Bernoulli, and d’Alembert in connection with problems on oscillation of strings. The study of it has played an essential role in the development of analysis.

2. The sequence of Legendre polynomials

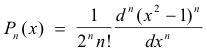
on the interval (-1, 1). The first few polynomials of the sequence are

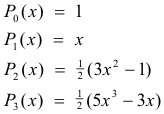
Def. Orthonormal system. A system of functions

is called orthonormal if it is orthogonal and if each of the functions is of unit length i.e.

Example. The sequence of trigonometric functions

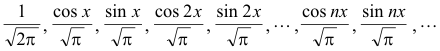
on the interval (-π, π) is orthonormal. These functions are obtained by dividing the functions

1, cos x, sin x, cos 2x, sin 2x, .... , cos nx, sin nx, .....

by their lengths.

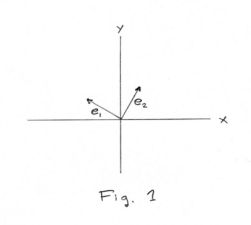
Expansion by orthogonal systems of functions. Let e₁ and e₂ be any two mutually perpendicular vectors of unit length in the plane. See Fig. 1. Then any vector f in the plane can decomposed in the direction of these two vectors and written as

f = a₁e₁ + a₂e₂

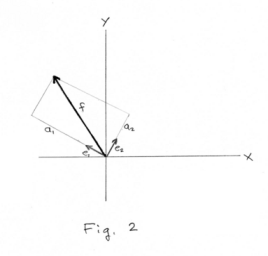
where a₁ = f•e₁ and a₂ = f•e₂ as shown in Fig. 2. Similarly if e₁, e₂ and e₃ are any three mutually perpendicular unit vectors in three-dimensional space any vector f in space can be decomposed in the direction of these three vectors and written as

f = a₁e₁ + a₂e₂ + a₃e₃

where a₁ = f•e₁, a₂ = f•e₂ and a₃ = f•e₃ .

Just as it is possible to represent any vector f in three-dimensional space as a linear combination

f = a₁e₁ + a₂e₂ + a₃e₃

of three pairwise orthogonal unit vectors it is possible to represent any function f in Hilbert space as a linear combination of an orthonormal system of functions. For this to be so, however, it is necessary for the orthonormal system to be complete.

Def. Complete orthogonal system. An orthogonal system of functions is called complete if it is impossible to add to it even one function, not identically equal to zero, that is orthogonal to all the functions of the system.

It is easy to give an example of an orthogonal system that is not complete. If we are given any arbitrary orthogonal system and remove a single function from it, the remaining system will be incomplete. Suppose, for example, that we remove cos x from orthogonal system

1, cos x, sin x, cos 2x, sin 2x, .... , cos nx, sin nx, .....

The remaining system

1, sin x, cos 2x, sin 2x, .... , cos nx, sin nx, .....

is orthogonal as before, but it is not complete since the function cos x which we excluded is orthogonal to all functions of the system.

Theorem 1. Let a complete orthonormal system of functions in Hilbert space

be given. Then every function f(x) in the space can be represented by a series

where the coefficients a_n of the expansion are equal to the projections of the vector f on the elements of the normal orthogonal system i.e.

Because of the analogy with Fourier series 1) is sometimes called a generalized Fourier series and the coefficients a_n generalized Fourier coefficients.

The formula above for a_n is easily derived. If we multiply both sides of 1) scalarly by any function f_n of the system, we get

Because f_m∙f_n= 0 for m ≠ n and f_n∙f_n = 1, equation 2) reduces to

Theorem 2 (Parseval’s identity). The square of the length of a vector in Hilbert space is equal to the sum of the squares of its projections onto a complete system of mutually orthogonal directions. In other words, if

are a complete orthonormal system of functions in Hilbert space and if a function f is given by

then

Proof

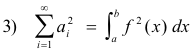
Condition of completeness. The condition of completeness for a functional space is that 3) hold for an arbitrary function of the space.

Analogue of the concept of completeness in n-dimensional space. In n-dimensional space any vector in the space can be expressed as a linear combination of n linearly independent basis vectors. However, not every vector in the space can be expressed as a linearly combination of only n-1 of the basis vectors. If one of the basis vectors is missing, not all vectors in the space can be expressed as a linear combination of the remaining basis vectors. The condition of completeness of an orthogonal system of functions corresponds to the requirement for a full set of n basis vectors for an n-dimensional space.

References

Mathematics, Its Content, Methods and Meaning. Vol. 3, Chap. XIX