Prove: Cauchy-Bunjakovski inequality. For any two arbitrary functions f(x) and g(x)

Proof. Let f(x) and g(x) be two functions, not identically equal to zero, given on the interval (a, b). Now choose two arbitrary numbers λ and μ and form the expression

Because the function [λf(x) - μg(x)]² under the integral sign is nonnegative, we have the following inequality

which, on expansion, is

which can be written as

We now introduce the notation

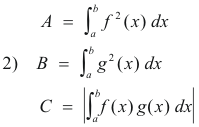
Using this notation 1) can be written as

3)        2λμC λ²A + μ²B 

Note. Using the absolute value for C in 2) is valid because λ and μ are of arbitrary sign. 

The inequality 3) is valid for arbitrary values of λ and μ. Consequently we may set

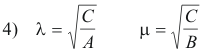
Substituting these values of λ and μ into 3) we get

If we now replace A, B and C by their expressions in 2) we obtain the Cauchy-Bunjakovski inequality.

Source: Mathematics, Its Content, Methods and Meaning. Vol. 3, p. 235