Hilbert space. Infinite-dimensional vectors. Inner product, orthogonal functions, Pythagorean theorem

SolitaryRoad.com

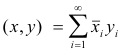
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Hilbert space. Infinite-dimensional vectors. Inner product, orthogonal functions, Pythagorean theorem.

Def. Hilbert space. A Hilbert space is a complete inner product space. In other words, it is a linear space on which an inner product has been defined and in which every Cauchy sequence converges to a point of the space. Usage varies but a Hilbert space is usually also required to be infinite-dimensional and separable. The most important realizations of a Hilbert space are:

(1) The set of all sequences of real or complex numbers (x₁, x₂, ... , x_n, .... ) such that (x₁² + x₂² + ... + x_n² ... ) is convergent. For two sequences x = (x₁, x₂, ... , x_n, .... ) and y = (y₁, y₂, ... , y_n, .... ) the sum x + y is defined as (x₁ + y₁, x₂ + y₂, ..... ), the product ax as (ax₁, ax₂, .... ), and the inner product as

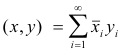
where the over-bar refers to the conjugate.

(2) The set of all (Lebesgue) measurable functions f on an interval [a, b] for which the integral of | f |² is finite (i.e. those functions for which the integral exists). Two functions are considered identical if they are equal almost everywhere on (a, b), the operations of addition and multiplication by scalars are defined as ordinary addition and multiplication, and the inner product (f, g) is defined as

A Lebesgue measurable function f for which the integral of | f |² is finite is said to be of class L² (L is abbreviation for Lebesgue). The set of all functions of class L² is called L² space. This class of functions includes most functions. It excludes some unusual or ill-behaved functions.

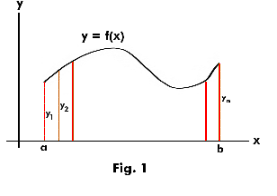
Functions viewed as vectors in infinite-dimensional space. In mathematical applications we may be given a function as a set of tabulated values e.g. temperature at some point on the earth as a function of time. In Fig. 1 the function y = f(x) is given as an ordered set of n values y₁, y₂, .... ,y_n at equally spaced increments on the interval [a, b]. The function y = f(x) can thus be identified with the n-dimensional vector (y₁, y₂, .... ,y_n). If we now allow the size of the subdivision to approach zero and n to approach , we can then view the function y = f(x) as a point in infinite-dimensional space.

Now if we view a function as a point in n-dimensional space we then have a means of describing the closeness of one function to another. We can use as a measure of the closeness of one function to another the distance between them in n-space (i.e. use the distance between two points in n-space).

Logical foundations of the functional space known as Hilbert space. Let us now consider the Hilbert space (2) described above. When we speak of Hilbert space we will be speaking of this space. The functions of this space are regarded as vectors in infinite-dimensional space. A vector of an n-dimensional space is defined as a set of n numbers f_i, where i ranges from 1 to n. In a similar way, a vector of an infinite-dimensional space is defined as a function f(x), where x ranges from a to b.

We now lay the logical foundations for the functional space called Hilbert space.

We start with the set of all (Lebesgue) measurable functions f on an interval [a, b] for which the Lebesgue integral of | f |² is finite i.e. L² space. If we assume for the functions of L² space that the operations of addition and multiplication by scalars are defined as ordinary addition and multiplication then the system qualifies as a linear space.

Our next step is to define a norm for the vectors i.e. a definition for the length of a vector. The length of a vector f in an n-dimensional space is defined as

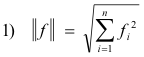
Since for functions the role of the sum is taken by the integral, we define the length of a vector f(x) of Hilbert space as

The system is now a normed linear space.

For information on linear spaces and normed linear spaces see Linear space (abstract vector space) and Normed linear spaces.

We now define a distance function for the space (which will turn it into a metric space). Any normed linear space can be turned into a metric space by defining on it the distance function

d(x, y) = || x - y ||

where x and y are vectors (or points) in the space and || x - y || is the norm of the vector x - y. This metric on a normed linear space is called the induced metric. The distance between points f and g in an n-dimensional space is defined as the length of the vector f - g, i.e. as

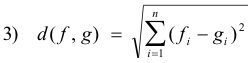
We define the distance between two points f(x) and g(x) in our functional space as

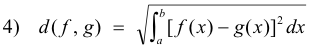
We now give a definition for the angle between two vectors in the space.

In an n-dimensional space the angle θ between the vectors f = {f _i} and g = {g_i} is defined by the formula

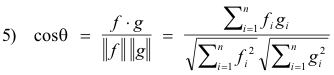
This formula is a direct generalization of the formula x•y = ||x|| ||y|| cos θ for three dimensional space. By the Schwarz inequality (theorem),

|x•y| ||x|| ||y||

for any two n-vectors x and y of n-space. Thus the fraction

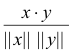
which corresponds to the right side of 5) is always in the range -1 to +1.

We now define the angle θ between two vectors f and g of Hilbert space by a formula analogous to 5), replacing sums by integrals:

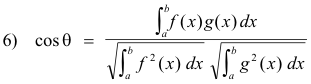
There is a theorem known as the Cauchy-Bunjakovski inequality that states that for any two arbitrary functions f(x) and g(x)

Proof

Thus the right side of 6) always has a value between -1 and 1.

We now note that 6) is also a generalization of the formula x•y = ||x|| ||y|| cos θ for three dimensional space. Using the formula for the norm given in 2) above we can replace the denominator on the right side of 6) with || f || || g || to give

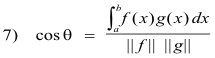
The numerator in the fraction represents the inner (or scalar or dot) product f •g of two functions f and g in Hilbert space i.e.

Def. Inner product of two vectors in Hilbert space. By definition, the inner (or scalar) product of two vectors f and g in Hilbert space is

The inner product of two vectors f and g in a functional space is generally denoted by (f, g), however we will use the dot notation f•g. For information on inner products see Inner product.

Orthogonal functions in Hilbert space. If the inner product of two nonzero vectors f and g in Hilbert space is equal to zero, it means that cos θ = 0 and the angle θ is 90^o. Consequently two functions f and g are called orthogonal if their inner (or scalar) product is zero i.e. if

Pythagorean theorem in Hilbert space. The Pythagorean theorem holds in Hilbert space just as it does in n-dimensional space. Let f₁(x), f ₂(x), .... , f_N(x) be N pairwise orthogonal functions and let

f(x) = f₁(x) + f ₂(x) + .... + f_N(x)

be their sum. Then the square of the length of f is equal to the sum of the squares of the lengths of f₁(x), f ₂(x), .... , f_N(x). Because the lengths of vectors in Hilbert space are given as integrals, the Pythagorean theorem in Hilbert space takes the form

Proof

References

James & James. Mathematics Dictionary

Mathematics, Its Content, Methods and Meaning. Vol. 3, p. 234 - 237