Compactness. Cover. Heine-Borel Theorem. Finite intersection property. Sequentially, countably and locally compact spaces. Bolzano-Weierstrass Theorem. Compactum. Compactification.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Def. Cover (of a set). A class C of sets is said to be a cover of a set S if every point of S belongs to some member of C.

Syn. Covering

Subcover. If C is cover of a set S and a subset Q of C is also a cover of S, then Q is called a subcover of S.

Open cover. If the members of a cover C are open sets the cover is called an open cover.

Finite subcover. If a finite subclass of a cover C of a set S is also a cover of S, then C is said to be reducible to a finite cover or to contain a finite subcover.

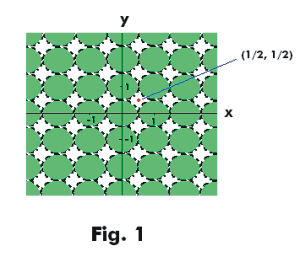
In the above definition we called C a class of sets. We could have used other words like set or collection but the term class seemed most appropriate. We speak of a class of people, a class of dogs, a class of vertebrates, etc. We mean some collection of things grouped together because of common properties. When we speak of a class of sets we are talking about some infinite collection of sets such as those depicted in Fig. 1. The class of sets shown in Fig. 1 is defined by

C = {D_p: p ε Z Z)

where D_p is the open disc in the plane R² with radius 1/2 and center at p = (m, n), m and n integers, Z the set of integers. The class of sets shown in Fig. 1 does not cover the plane but if we increase the radius of the discs to, say, r = 1, then it does cover the plane.

We shall now treat the concept of a compact set. The idea of a compact set derives from the Heine-Borel Theorem. So let us consider the Heine-Borel Theorem.

Heine-Borel Theorem. If an infinite set C of open intervals covers the finite closed interval [a, b] in the sense that every point of [a, b] is contained in at least one interval of C, then there exists a finite subset of C having the same property.

We must consider the wording of this theorem carefully. This theorem is not asserting the existence of a finite open cover for the interval [a, b]. That is not what it is about. If you have a closed interval [2, 5] it is obvious that a finite cover consisting of a single open interval (1, 6) would cover it. Rather, the theorem is about the nature and properties of covers (infinite sets of open intervals) and the circumstances under which they will contain a finite subcover for a particular set of points (more precisely, the circumstances under which every open cover contains a finite subcover). The statement made by the Heine-Borel Theorem is true for the closed interval [a, b]. It is not true for the open interval (a, b). We can reword the Heine-Borel Theorem as follows:

Heine-Borel Theorem. Every class of open intervals of the real line R whose union contains the finite closed interval [a, b] contains a finite subclass whose union also contains [a, b]. Or using the language of covers: Every open cover of the finite closed interval [a, b] contains a finite open subcover.

We will now show that every open cover of the open interval (a, b) does not contain a finite open subcover. To do this we need only exhibit a single case where a cover of a set (a, b) does not possess a finite open subcover.

Example 1. Consider the open interval A = (0, 1). Observe that the class of open intervals

given by

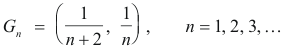
covers A. See Fig. 2. However, G contains no finite subcover. To show this let

G* = {(a₁, b₁), (a₂, b₂), .... , (a_m, b_m)}

be any finite subclass of G. If ε = min (a₁, a₂, ..., a_m) then ε > 0 and

Now (0, ε] and (ε, 1) are disjoint and so G* is not a cover of A.

Def. Compact space. A topological space is called compact if every open cover has a finite subcover.

Def. Compact set. A subset S of a topological space is called compact if every open cover of S has a finite subcover.

● By the Heine-Borel Theorem every closed and bounded interval [a, b] on the real line R is compact.

● Any finite subset of a topological space is compact.

Example 2. Let A be any finite subset of a topological space X. Then A is necessarily compact. To show this let A = {a₁, a₂, .... , a_m) and let G = {G_i} be an open cover of A. Then each point in A belongs to one of the members of G, say

Consequently

Theorem 1. Continuous images of compact sets are compact.

Subsets of compact spaces. A subset of a topological space need not be compact. For example, the closed interval [a, b] is compact by the Heine-Borel Theorem, but the open interval (a, b) which is a subset of [a, b] is not compact.

Theorem 2. Any closed subset of a compact space is compact.

Finite intersection property. For a collection of sets to have the finite intersection property means that each nonempty finite subcollection of these sets has a nonempty intersection.

James & James. Mathematics Dictionary

Example 3. Consider the following collection of open intervals:

M has the finite intersection property since for any finite subcollection {(0, a₁), (0, a₂), .... ,(0, a_m) }

(0, a₁) (0, a₂) (0, a_m) = (0, b)

where b = min(a₁, a₂, ...., a_m). Note that M itself has an empty intersection.

Theorem 3. A topological space X is compact if and only if every collection of closed subsets of X with the finite intersection property has a nonempty intersection.

In Example 3 above we have an example in which the collection M of open sets has the finite intersection property but M itself has an empty intersection. In Theorem 3 it is required that every collection with the finite intersection property has a nonempty intersection.

Theorem 4. All compact subsets of a Hausdorff space are closed.

Theorem 5. Every compact Hausdorff space is normal.

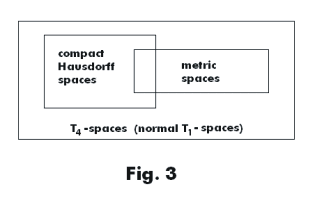
The metric spaces and compact Hausdorff spaces are both contained in the class of T₄-spaces. See Fig. 3.

Theorem 6. Let f be a one-to-one continuous function from a compact space X into a Hausdorff space Y. Then X and f(X) are homeomorphic.

Example 4. Let f be a one-to-one function from the closed interval I = [0, 1] into Euclidean n-space Rⁿ. I is compact by the Heine-Borel Theorem and Rⁿ is a metric space and therefore Hausdorff. Thus I and f(I) are homeomorphic.

Def. Sequentially compact space. A topological space X is sequentially compact if every sequence in X contains a subsequence which converges to a point in X.

Sequentially compact set. A subset A of a topological space X is sequentially compact if every sequence in A contains a subsequence which converges to a point in A.

Example 5. The open interval A = (0, 1) on the real line R with the usual topology is not sequentially compact. Consider, for example, the sequence

in A. Note that {s_n} converges to 0 and therefore every subsequence also converges to 0. However, 0 does not belong to A. In other words, the sequence {s_n} does not contain a subsequence that converges to a point in A. Consequently A is not sequentially compact.

Def. Countably compact space. A countably compact topological space is a space X with the property that, for any union of a countable number of open sets that contains X, there is a finite number of these open sets whose union contains X.

Theorem 7. A topological space X is countably compact if and only if each sequence in X has an accumulation point in X.

Countably compact set. A subset A of a topological space X is countably compact if and only if each sequence in A has an accumulation point in A.

Bolzano-Weierstrass Theorem. Every bounded infinite set Q of real numbers has at least one accumulation point.

Note. The accumulation point need not be within the set Q.

Example 6. Every bounded closed interval A = [a, b] is countably compact. Why? Let B be an infinite subset of A. Then B is also bounded and, by the Bolzano-Weierstrass Theorem, has an accumulation point p. Moreover, since A is closed, the accumulation point p belongs to A. Thus A is countably compact.

Example 7. The open interval A = (0, 1) is not countably compact. Why? Consider the infinite subset

of A = (0, 1). Note that B contains exactly one limit point which is 0 and that 0 does not belong to A. Thus A is not countably compact.

Theorem 8. Let A be a subset of a topological space. If A is compact or sequentially compact, then A is countably compact.

Theorem 9. For a Lindelof space (and therefore also for a metric space) compactness, sequential compactness and countable compactness are equivalent. Each implies the others.

Def. Locally compact space. A topological space is locally compact if every point has a compact neighborhood.

Example 8. The real line R with the usual topology is not compact. However, it is locally compact. Reason: Note that each point p ε R is interior to a closed interval , e.g. [p - δ, p + δ], and that the closed interval is compact by the Heine-Borel Theorem.

R is not compact. For example, the collection

A = { ..... , (-3, -1), (-2, 0), (-1, 1), (0, 2), (1, 3), ..... }

is an open cover of R but contains no finite subcover.

Thus we see that a locally compact space need not be compact. However, every compact space is locally compact.

Theorem 10. Every compact space is locally compact.

Def. Compactum. A topological space which is compact and metrizable. Examples of compacta are closed intervals, closed spheres (with or with out their interiors), and closed polyhedra.

James & James. Mathematics Dictionary

Compactification. A topological space X is said to be embedded in a topological space Y if X is homeomorphic to a subspace of Y. In addition, if Y is a compact space, Y is called a compactification of X. Often the compactification of a space X is accomplished by adjoining one or more points to X and then defining an appropriate topology on the enlarged set so that the enlarged space is compact and contains X as a subspace.

Example 9. Consider the real line R with the usual topology τ. We adjoin two new points, denoted by and - , to R and call the enlarged set R* the extended real line. The collection of subsets of R* of the form (a, b), (a, ) and [- , a) is a base for a topology τ* on R*. (R*, τ*) is compact and contains (R, τ) as a subspace. It thus represents a compactification of (R, τ).

References

1. Lipschutz. General Topology

2. Simmons. Introduction to Topology and Modern Analysis

3. Munkres. Topology, A First Course

4. James & James. Mathematics Dictionary