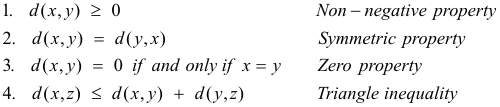
Website owner: James Miller
Metric spaces. Examples. Convergence of sequences. Cauchy’s condition for convergence. Complete metric space. Cantor’s Intersection Theorem. Dense sets. Continuous mappings.
Def. Metric space. A metric space consists of a set M of arbitrary elements, called points, between which a distance is defined i.e. a number d(x, y) is associated with each pair of points x, y so that the following conditions, namely the axioms of a metric space, are satisfied:
A metric space is an abstract mathematical system, a generalization/ abstraction of three dimensional Euclidean space. The above properties correspond to certain central properties of distances in three dimensional Euclidean space. The distance d(x, y) that is defined between “points” x and y of a metric space is called a metric or distance function.
The distance function associated with a metric space may be a naturally occurring one as in the case of the usual Euclidean spaces of one, two or three dimensions or it may be a man-defined one as in the case of a functional space. It often happens that several different metrics can be defined on a set of elements giving different metric spaces. Thus a metric space is more than just the underlying set M of elements. It is the set M along with a specified distance function (or metric).
Examples of metric spaces
1. The real line. The set R of all real numbers in which the distance function is the usual distance between points on the real line given by d(x, y) = |x - y|. This metric is called the usual metric on R.
2. Two dimensional Euclidean space. The set of all points (x, y) of two dimensional Euclidean space with a distance function defined by
![]()
where P1(x1, y1) and P2(x2, y2) are any two points of the space. This metric is called the usual metric in R2.
3. Three dimensional Euclidean space. The set of all points (x, y, z) of three dimensional Euclidean space with a distance function defined by
![]()
where P1(x1, y1, z1) and P2(x2, y2, z2) are any two points of the space. This metric is called the usual metric in R3.
4. N-dimensional Euclidean space. The set of all points of n-dimensional Euclidean space with a distance function defined by
![]()
where x = (x1, x2, ..... , xn) and y = (y1, y2, ..... , yn) are any two points of the space.
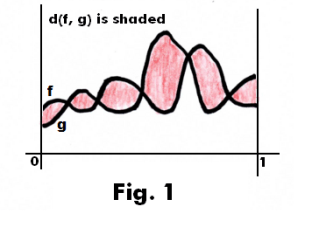
5. Space C [0, 1] of continuous functions with Metric 1. Let C [0,1] denote the collection of all continuous functions on the closed interval [0, 1]. The collection of continuous functions C [0,1] with the metric
![]()
is a metric space. d(f, g) is the area shaded in Fig. 1.
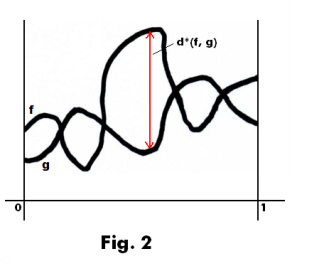
6. Space C [0, 1] of continuous functions with Metric 2. Let C [0,1] denote the collection of all continuous functions on the closed interval [0, 1]. The collection of continuous functions C [0,1] with the metric
d*(f, g) = max { | f(x) - g(x) | : x ε [0, 1] }
is a metric space. d*(f, g) is the greatest vertical gap between the functions as shown in Fig. 2.
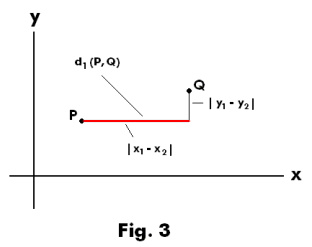
7. Two other metric spaces in the plane. Let P(x1, y1) and Q(x2, y2) be two arbitrary points in the plane R2. The functions d1 and d2 defined by
d1(P, Q) = max ( |x1 - x2|, |y1 - y2| )
and
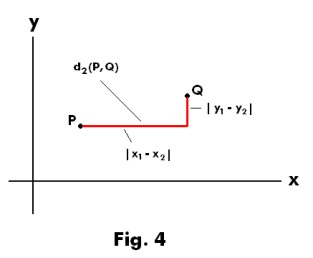
d2(P, Q) = |x1 - x2| + |y1 - y2|
represent two distinct metrics on R2. See Figs. 3 and 4.
8. Any surface in its intrinsic measure.
9. Hilbert space.
Normed linear spaces as metric spaces. The metric spaces of Examples 1 - 5 above are all normed linear spaces. Most of the spaces of major importance in analysis are normed linear spaces. For information on normed linear spaces see the following:
Any normed linear space can be turned into a metric space by defining on it the distance function
d(x, y) = || x - y ||
where x and y are vectors (or points) in the space and || x - y || is the norm of the vector x - y. This metric on a normed linear space is called the induced metric.
Concepts: distance idea, continuum of points. Let us give some thought to the concept or idea of distance. What is distance? We are all familiar with the idea of the distance between two points in space.
First let us look at the dictionary definition.
Def. Distance. The extent of spatial separation between things, places or locations.
Funk & Wagnalls Dictionary
Def. Space. That which is characterized by dimensions extending indefinitely in all directions and within which all material bodies are located.
Funk & Wagnalls Dictionary
The concept of distance is intricately tied to the concept of a continuum of points. And closely connected with the ideas of distance and a continuum is the idea of adjacency, being “infinitely near” to something. In the above dictionary definition distance is defined as the extent of spatial separation between objects. Well, the amount of separation can be anything from infinitely small to infinitely large. That implies a continuum of possible distances. If a distance concept exists that is similar to the familiar distance from three dimensional space, then a continuum of distances will exist. If a distance concept doesn’t exist, a continuum concept can’t exist.
Origin of idea of a created metric or distance. Where did the concept of a metric space come from? Where did the idea of inventing a metric or distance function for a space of points come from? Presumably it arose with the idea of n-tuples. If we consider the set of all points (x, y, z) satisfying
![]()
![]() x
x
![]()
![]()
![]()
![]() y
y
![]()
![]()
![]()
![]() z
z
![]()
![]()
they represent the three dimensional continuum of points constituting what we know as three dimensional space.. If we consider the set of all points (x1, x2, x3, x4) satisfying
![]()
![]() x1
x1
![]()
![]()
![]()
![]() x2
x2
![]()
![]()
![]()
![]() x3
x3
![]()
![]()
![]()
![]() x4
x4
![]()
![]()
it is natural to wonder if we could interpret them as a four dimensional continuum similar to the three dimensional continuum of 3-space. However, in the case of the points in 3-space there is a natural distance defined between points but in the case of the set of the points (x1, x2, x3, x4) this is not so. Without a distance how can they form a continuum? The question naturally presents itself as to whether it might be possible to define a distance for 4-tuples — or, in general, for n-tuples. The answer to the question was shown to be in the positive, that it was indeed possible, and that the distance formula used for 3-space could be used unchanged for n-space. Thus the first space with an artificial, invented distance was created i.e. the first metric space was created. With the defined distance the space of n-tuples became a continuum. Later in the study of the properties of functions it was realized that a distance could be defined on the set of all continuous functions on the interval [a, b] and they could be turned into a metric space. I have only guessed at the likely scenario.
Model for a metric space. The model for a metric space is the regular one, two or three dimensional space. A metric space is any space in which a distance is defined between two points of the space.
Two dimensional space can be viewed as a rectangular system of points represented by the
Cartesian product R
![]() R [i.e. all number pairs (x, y) where x ε R, y ε R]. Three dimensional
space can be viewed as a three-dimensional system of points represented by the Cartesian
product R
R [i.e. all number pairs (x, y) where x ε R, y ε R]. Three dimensional
space can be viewed as a three-dimensional system of points represented by the Cartesian
product R
![]() R
R
![]() R [i.e. all number pairs (x, y, z) where x ε R, y ε R, z ε R].
R [i.e. all number pairs (x, y, z) where x ε R, y ε R, z ε R].
It was observed that the distance d(x, y) between any two points x and y in ordinary one, two or three dimensional space has the following algebraic properties.:
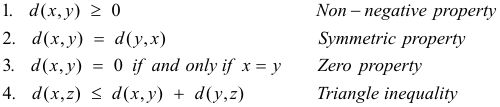
The idea was then conceived of defining a “distance” with these algebraic properties in spaces like n-dimensional space that don’t possess a natural concept of distance. Thus n-space in which a “distance” has been defined was presumably the first “metric space” (a space other than regular space containing an artificially defined distance). It was then realized that one could do the same thing with other spaces (such as functional spaces) and the mathematical structure of axiomatically defined metric space was conceived.
Let us now observe something. What conception can we have of a metric space? Can we view it as a continuum of points with a “distance” defined between pairs of points as is the case for two, three and n-dimensional spaces? The definition states that it is “an arbitrary set of elements (or points)” with a distance defined between pairs with the given properties. It doesn’t say that the points have to be from a continuum. With these axiomatic definitions any mathematical system that meets the axiomatically phrased definition qualifies. In fact, we can exhibit a finite set of discrete elements with a defined distance that meets the requirements of the definition. The following meets the requirements:
Example of a metric space with discrete elements. Let X be any non-empty set and let d be the function defined by
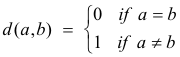
Then d is a metric on X. This is called the trivial metric on X.
We see from this example that axiomatic, property-oriented, definitions can lead to things radically different in character from the model from which the definitions were generalized. One uses a axiomatic definition to define a horse and the definition presents him with turkeys and snakes. The distance on this metric space is a radically different animal from the usual distance on three dimensional space. The points on this space do not form a continuum.
Note. In modern mathematics that continuum constituting a line (straight or curved) is viewed as simply a collection of points. Similarly the continuum of a plane (or curved surface) is viewed as simply a collection of points. And the space within a sphere or other solid figure (a three dimensional continuum) is also viewed as a collection of points. These are all different types of continua. The validity of viewing a continuum as simply a collection of points is not at all obvious to me. I think the validity of doing it would be questioned by anyone first introduced to the idea.
Metric space definitions
*************************************************************************
Def. ε-neighborhood of a point. The ε-neighborhood of a point P is the open set consisting of all points whose distance from P is less than ε. We note that the boundary is not included. Another name for ε-neighborhood is open sphere. Other names are spherical neighborhood and ball. The open sphere at point p is denoted by S(p, ε).
Def. ε-deleted neighborhood of a point. The ε-deleted neighborhood of a point P is the ε- neighborhood of the point P minus the point P itself.
Def. Neighborhood of a point. A neighborhood of a point P is any set that contains an ε-neighborhood of P.
Note. We see, from the definitions, that while an ε-neighborhood of a point is an open set a neighborhood of a point may be open, closed or neither open nor closed..
Def. Interior point of a point set. A point P is called an interior point of a point set S if there exists some ε-neighborhood of P that is wholly contained in S.
Def. Boundary point of a point set. A point P is called a boundary point of a point set S if every ε-neighborhood of P contains points belonging to S and points not belonging to S.
Def. Exterior point of a point set. A point P is an exterior point of a point set S if it has
some ε-neighborhood with no points in common with S i.e. a ε-neighborhood that lies wholly in
![]() , the complement of S. If a point is neither an interior point nor a boundary point of S it is an
exterior point of S.
, the complement of S. If a point is neither an interior point nor a boundary point of S it is an
exterior point of S.
Def. Limit point. A point P is called a limit point of a point set S if every ε-deleted neighborhood of P contains points of S.
Def. Derived set. The set of all limit points of a set S is called the derived set and is
denoted by
![]() .
.
Def. Isolated point. A point of a point set in whose neighborhood there is no other point of the set.
Def. Open set. A point set is said to be open if each of its points is an interior point.
Def. Closed set. A point set is called closed if it contains all of it limit points.
*************************************************************************
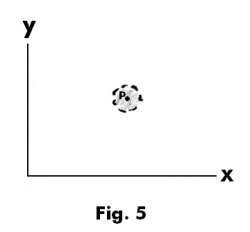
Example 1. The ε-neighborhood of a point P in the plane is the open disk shown in Fig. 5.
Example 2. Let d be the metric on the collection C [0,1] of all continuous functions on [0,1] defined by
d(f, g) = max { | f(x) - g(x) | : x ε [0, 1] }
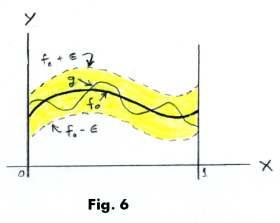
Given ε > 0 and a function f0 ε C [0,1], then the ε-neighborhood of point f0 consists of all continuous functions g which lie in the area bounded by f0 - ε and f0 + ε as shown in Fig. 6.
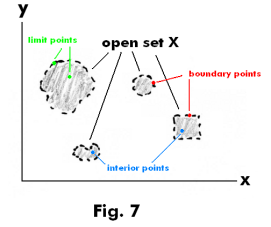
Example 3. In Fig. 7 are shown some interior points, limit points and boundary points of an open point set in the plane.
Distance between a point and a set in a metric space. Let d be a metric on a set M. The distance d(p, A) between a point p ε M and a non-empty subset A of M is defined as
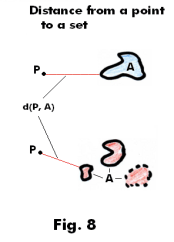
d(p, A) = inf {d(p, a): a ε A}
i.e. the greatest lower bound of the distances from p to points of A. In other words, it is the distance from p to the closest point of A. See Fig. 8.
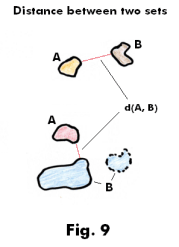
Distance between two sets in a metric space. Let d be a metric on a set M. The distance d(A, B) between two non-empty subsets A and B of M is defined as
d(A, B) = inf {d(a, b): a ε A, b ε B}
i.e. the greatest lower bound of the distances from points in A to points in B. See Fig. 9.
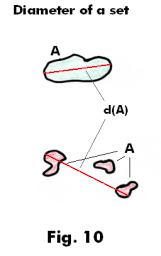
Diameter of a set in a metric space. Let d be a metric on a set M. The diameter d(A) of a non-empty subset of M is defined as
d(A) = sup {d(a, a'): a, a' ε A}
i.e. the least upper bound of the distances between points in A. See Fig. 10.
If the diameter of A is finite, i.e. d(A) <
![]() , then A is said to be bounded. If not, then A is said
to be unbounded.
, then A is said to be bounded. If not, then A is said
to be unbounded.
Theorem 1. Let A and B be non-empty subsets of a set M with metric d. Let p ε M. Then
1) d(p, A), d(A, B) and d(A) are non-negative real numbers.
2) If p ε A, then d(p, A) = 0.
3) If A
![]() B in non-empty, then d(A, B) = 0.
B in non-empty, then d(A, B) = 0.
4) If A is finite, then d(A) <
![]() i.e. A is bounded.
i.e. A is bounded.
Conventions involving the empty set ∅:
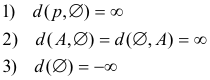
Theorem 2. In any metric space M, each open sphere is an open set.
Theorem 3. Let M be a metric space. A subset G of M is open
![]() M is a union of open spheres.
M is a union of open spheres.
Theorem 4. Let M be a metric space. Then
1) any union of open sets in M is open
2) any finite intersection of open sets in M is open
This theorem tells us that the collection of all open sets in a metric space M form a closed system with respect to the operations of union and intersection.
The collection τ of all open sets in a metric space M doesn’t represent all possible sets that can be formed on M. Let π be the set of all possible sets that can be formed on M. The union or intersection of any two sets in π is a set in π. The union or intersection of any two sets in τ is a set in τ. τ represents some subset of π that is closed with respect to the operations of union and intersection. Thus we have here a situation that is analogous to a subgroup of a group or a subspace of a vector space where the elements of some subset of a larger set form a closed system (with respect to an operation) and are thus a closed system embedded within a larger closed system.
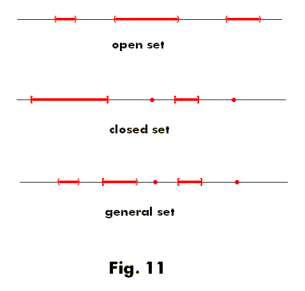
For insight and clearer understanding of the concepts look to the point sets of one, two and three dimensional spaces for a model from which to think. Let M be the real line and τ be the set of all open sets in M. In Fig. 11 is depicted a typical open set, closed set and general set (neither open nor closed) on the real line. The set π corresponds to all possible unions and intersections of general sets in M. The union or intersection of any two open sets in M is open. Thus the collection of all open sets in M form a closed system with respect to the operations of union and intersection. They constitute a subset τ of the collection of all possible sets π in M.
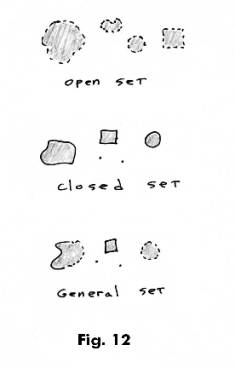
We can also let M be the set of all points in the plane. Fig. 12 shows typical open, closed and general sets in the plane. The same comments apply.
The limitation to finite intersections in Theorem 4 cannot be removed. To see why consider the following sequence of open intervals on the real line:
(-1, 1), (-1/2, 1/2), (-1/3, 1/3), .....
The intersection of these open sets is the set {0} consisting of the single point 0, and this set is not open.
Theorem 5. Let M be a metric space. A
subset G of M is closed
![]() its complement G' is open.
its complement G' is open.
Closed sphere. A closed sphere is a sphere that contains all of its limit points i.e. it is an open
sphere plus its boundary points. A closed sphere of radius ε centered at point P consists of all
points whose distance from P is
![]() ε .
ε .
Theorem 6. In any metric space M, each closed sphere is a closed set.
Theorem 7. Let M be a metric space. Then
1) any union of closed sets in M is closed
2) any finite intersection of closed sets in M is closed
The empty set ∅ and the full set M are both open and closed. In order for Theorems 4 and 7 to be valid it is necessary to assume that empty set ∅ and the full set M are both open and closed. Let us see why this is true. The intersection of two disjoint open sets is the null set ∅. Thus, by Theorem 4, the null set ∅ is open. From this we deduce from Theorem 5 that the full set M is closed. Now the intersection of two disjoint closed sets is also the null set ∅. Thus, by Theorem 7, the null set ∅ is closed. From this we deduce from Theorem 5 that the full set M is open.
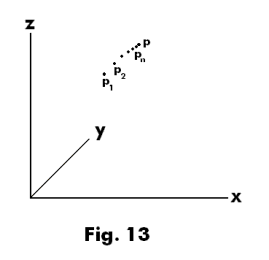
Convergence of sequences of points in metric spaces. Let M be a metric space with metric d and let {p1, p2, p3, .... , pn, ....} be a sequence of points within M. Fig. 13 depicts such a sequence in three dimensional space. Such a sequence will converge to a point p ε M under the following condition:
1) for each ε > 0, there exists a positive integer n0 such that n
![]() n0
n0
![]() d(pn, p) < ε
d(pn, p) < ε
or equivalently,
2) for each open sphere Sε(p) centered on p, there exists a positive integer n0 such that pn is in
Sε(p) for all n
![]() n0
n0
We have illustrated with an example of points in 3-space but the sequence {pn} could also, for example, be a sequence of functions in a function space.
If a sequence converges to a point p, it is said to have the limit p. If a sequence {pn} converges to a point p we write
pn → p
or
lim pn = p
and say pn approaches p, pn converges to p, or the limit of pn is p.
Cauchy’s condition for convergence of a sequence. An infinite sequence converges if, and only if, the numerical difference between every two of its terms is as small as desired, provided both terms are sufficiently far out in the sequence. Tech. The infinite sequence s1, s2, s3, ... , sn, ... converges if, and only if, for every ε > 0 there exists an N such
| sn+h - sn | < ε
that for all n > N and all h > 0.
James and James. Mathematics Dictionary
Def. Cauchy sequence. A Cauchy sequence is a sequence where, given any preassigned positive number ε, however small, there exists a point in the sequence (possibly very far out) beyond which the distance between any two selected elements is less than ε. Tech. A Cauchy sequence is a sequence of points P1, P2, ... such that for any ε > 0 there is a number N for which ρ(Pi, Pj) < ε if i > N and j > N, where ρ(Pi, Pj) is the distance between Pi and Pj. If the points are points of Euclidean space, this is equivalent to the sequence being convergent. If the points are real (or complex) numbers, then ρ(Pi, Pj) is | Pi - Pj | and the sequence is convergent if and only if it is a Cauchy sequence.
Syn. Convergent sequence, fundamental sequence, regular sequence.
James and James. Mathematics Dictionary
Def. Complete metric space. A metric space such that every Cauchy sequence converges to a point of the space.
The space of all real numbers (or of all complex numbers) is complete but the space of all rational numbers is not complete. The space of all continuous functions defined on the interval [0, 1] is not complete if the distance between f and g is defined as is
![]()
since the sequence f1, f2, ..... does not then converge to a continuous function if fn(x) = 0 for
0
![]() x
x
![]() 1/2 and
1/2 and
![]()
for 1/2
![]() x
x
![]() 1.
1.
James and James. Mathematics Dictionary
The space of all continuous functions defined on the interval [0, 1] is complete if the distance between f and g is defined as is
d(f, g) = max { | f(x) - g(x) | : x ε [0, 1] }
Theorem 8. Let X be a complete metric space and let Y be a subspace of X. Then Y is
complete
![]() Y is closed.
Y is closed.
Def. Decreasing sequence of sets. A sequence {An}of subsets of a metric space is called a decreasing sequence if
![]()
Cantor’s Intersection Theorem. Let X be a complete metric space and let {Gn} be a
decreasing sequence of non-empty closed subsets of X such that d(Gn)
![]() 0. Then
0. Then
![]()
contains exactly one point.
Def. Dense set. A set E in a space M is dense (or dense in M, or everywhere dense) if every point of M is a point of E or a limit point of E, or (equivalently) if the closure of E is M, or if every neighborhood in M contains a point of E. A set E is dense in itself if every point of E is an accumulation point of E; i.e. if each neighborhood of any point of E contains another point of E.
Example. The set of rational numbers is dense in itself and dense in the set R of all real numbers, as is also the set of irrational numbers. This is equivalent to the fact that between any two real numbers (either rational or irrational) there both rational and irrational numbers.
James & James. Mathematics Dictionary
Def. Nondense set. A set E in a space M is nondense (or nowhere dense) relative to M if the closure of E contains no interior points, or (equivalently) if the complement of the closure of E is dense in M.
Example. The set S = {0, 1, 1/2, 1/3, 1/4, .....} is nowhere dense in R, since 0 is the only accumulation point of S and the closure of S contains no interior points.
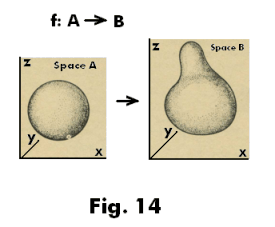
Continuous mappings. The subject of topology is much interested with continuous mappings of figures. In Fig. 14 a sphere is carried into a pear shape by a bicontinuous, bijective (one-to-one, onto) mapping. What conditions must a mapping meet in order to be continuous? The answer is as follows.
Def. Continuous mapping. Let X and Y be metric spaces with metrics d1 and d2, and let f be a mapping of X intoY. The mapping f is said to be continuous at a point p0 in X if either of the following equivalent conditions are satisfied:
1) for each ε > 0 there exists δ > 0 such that d1(p, p0) < δ
![]() d2(f(p), f(p0)) < ε
d2(f(p), f(p0)) < ε
2) for each open sphere Sε(f(p0)) centered on f(p0) there exists an open sphere Sδ(p0) centered on
p0 such that f(Sδ(p0))
![]() Sε(f(p0)) .
Sε(f(p0)) .
A mapping f of one metric space into another is said to be continuous if it is continuous at each point of its domain.
Theorem 9. Let X and Y be metric spaces and f a mapping of X into Y. Then f is continuous
at p0 if and only if pn
![]() p0
p0
![]() f(pn)
f(pn)
![]() f(p0).
f(p0).
Theorem 10. Let X and Y be metric spaces and f a mapping of X into Y. Then f is
continuous if and only if pn
![]() p
p
![]() f(pn)
f(pn)
![]() f(p).
f(p).
This result shows that continuous mappings of one metric space into another are precisely those which send convergent sequences into convergent sequences. In other words, they are those mappings which preserve convergence.
Theorem 11. Let X and Y be metric spaces and f a mapping of X into Y. Then f is
continuous
![]() f-1(G) is open in X whenever G is open in Y.
f-1(G) is open in X whenever G is open in Y.
Theorem 12. Let X and Y be metric spaces and f a mapping of X into Y. Then f is
continuous
![]() f-1(G) is closed in X whenever G is closed in Y.
f-1(G) is closed in X whenever G is closed in Y.
In other words, a function f is continuous if and only if the inverse of each open set in the range R is open in the domain D (or if and only if the inverse of each closed set in R is closed in D).
Def. Uniformly continuous mapping. If X and Y are metric spaces with metrics d1 and
d2, then a mapping f of X into Y is said to be uniformly continuous if for each ε > 0 there exists δ
> 0 such that d1(p, p' ) < δ
![]() d2(f(p), f(p' )) < ε.
d2(f(p), f(p' )) < ε.
In regular continuity δ depends not only on ε but also on the point p0. Uniform continuity is essentially continuity plus the added condition that for each ε we can find a δ which works uniformly over the entire space X, in the sense that it does not depend on p0.
Theorem 13. Let X be a metric space, let Y be a complete metric space, and let A be a dense subspace of X. If f is a uniformly continuous mapping of A into Y, then f can be extended uniquely to a uniformly continuous mapping g of X into Y.
References
1. James & James. Mathematics Dictionary.
2. Mathematics, Its Content, Methods and Meaning. Vol. III
3. Lipschutz. General Topology.
4. Simmons. Introduction to Topology and Modern Analysis.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life