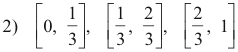
Prove. The closed interval U = [0, 1] is non-denumerable.

Proof. Let us assume the contrary. Assume the interval U = [0, 1] is a denumerable set. Then all of its points can be arranged in a sequence

1)        x₁, x₂, x₃, ......

We thus assume that every point x ε U occurs in the sequence 1). Now divide U into three equal parts by means of the points 1/3 and 2/3 giving the intervals

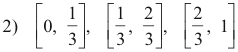
Now x₁ cannot belong to all three intervals (if it is an endpoint it could belong to two of the intervals). Denote by U₁ the interval that does not contain x₁. Now divide the interval U₁ into three sub-intervals of equal length and denote by U₂ the interval that does not contain x₂. Now divide U₂ into three sub-intervals of equal length and denote by U₃ the interval that does not contain x_3. If we continue in this manner we obtain an infinite sequence of nested intervals

which possesses the property that

We thus end up with an interval U_n that contains no points. Now the length of the interval U_n is 1/3ⁿ so it is clear that this length approaches zero as n . Now this result that we have obtained, an interval U_n that contains no points, stands in contradiction to the result predicted by Cantor’s Principle which states that there will be one point ζ belonging to all the intervals in such a nested system. We have thus reached a contradiction and conclude that our hypothesis that the interval U = [0, 1] is a denumerable set is false. Thus it must be non-denumerable.