Open sentences. Reflexive, symmetric, transitive and equivalence relations. Equivalence class. Truth set.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Def. Open sentence. A open sentence is an expression containing one or more variables which is either true or false depending on the values of the variables e.g. the statement x > 5 which is true if x = 7 and false if x = 3.

Synonyms. Open statement, statement function, propositional function, sentential function.

Examples.

1) x is the father of y

2) x is the spouse of y

3) 3x² + 5y - 3z = 0

4) x is a river in China

5) x is a citizen of y

Def. Relation. Equality, inequality or any property that can be said to hold (or not hold) for two objects in a specified order. In an open sentence of the form xRy, R stands for the relation “=”, “≠”, “>”, “<“, “is the father of”, “is the spouse of”, “is the grandson of”, etc. as in the following examples:

x = y

x≠y

x > y

x < y

x is the father of y

x is the spouse of y

x is the grandson of y

x is a friend of y

x is older than y

x likes y

***********************************************************************

Reflexive, symmetric, transitive, equivalence relations. Relations are categorized as

1) reflexive, anti-reflexive and non-reflexive

2) symmetric, antisymmetric, and nonsymmetric

3) transitive, intransitive and nontransitive

as follows:

Reflexive relation. A relation where xRx for all x.

Example. The relation "is equal to" on the set of real numbers, since every real number is equal to itself.

Anti-reflexive relation. A relation for which xRx is not true for any x.

Example. The "greater than" relation on the real numbers since it is not true for any x that x > x.

Non-reflexive relation. A relation that is partially, but not wholly reflexive, in that for some cases xRx, but not in all cases.

Example. The relation “is the reciprocal of”, since x is the reciprocal of x if x is +1 or -1, but otherwise x is not the reciprocal of x.

Symmetric relation. A relation R with the property that if x is related to y , then y is related in the same way to x i.e. xRy implies yRx.

Examples.

1) The equals relation in algebra: x = y.

2) “is the spouse of”. If x is the spouse of y, then y is the spouse of x.

Antisymmetric relation. A relation R for which if xRy, then always yRx is not true.

Example. The relation “is the father of ”. If x is the father of y, then y is not the father of x.

Nonsymmetric relation. A relation that is partially, but not wholly symmetric, in that for some cases both xRy and yRx, but not in all cases.

Example. The relation “likes” in “x likes y” — x may like y but y may or may not like x.

Transitive relation. A relation is transitive if xRy and yRz implies xRz.

Examples.

1) The relation of equality in arithmetic, since if x = y and y = z, then x = z.

2) The relations “is greater than” and “is less than”

3) The relation “is the ancestor of”

Intransitive relation. A relation is intransitive if when xRy and yRz, then always x z.

Example. The relation “is the father of”. If x is the father of y and y is the father of z, then x is never the father of z.

Nontransitive relation. A relation that is partially, but not wholly transitive, in that for some cases if xRy and yRz, then xRz, but not in all cases.

Example. The relation “is a friend of”. If x is a friend of y and y is a friend of z, then x may or may not be a friend of z.

***********************************************************************

Def. Equivalence relation. A relation between elements of a given set which is a reflexive, symmetric, and transitive. In other words, a relation R on a set M is an equivalence relation on M if, for elements a, b, c ε M,

1) aRa for all a ε M

2) if aRb, then bRa

3) if aRb and bRc, then aRc

An equivalence relation is also called an equals relation, and one says that two objects are equivalent or equal with respect to that equivalence relation e.g. triangles may be said to be equal if they are congruent, or if they are similar, or if they have the same area.

Examples of equivalence relations.

1) ordinary equality

2) similarity of triangles

3) congruence of triangles

4) “has the same surname as”

5) the relations of equivalence, congruence and similarity for matrices

6) relation of congruence modulo n for integers

Equivalence classes. Let R be an equivalence relation on a set S. Then R partitions S into mutually disjoint subsets of equivalent elements called equivalence classes where any two elements of S belong to the same equivalence class if and only if they are equivalent. Two equivalence classes are identical if they have an element in common. Every element of S belongs to one of the equivalence classes. In some cases these equivalence classes may be regarded as a new mathematical entity. For example, a set of equivalent fractions is called a rational number.

Examples.

1) Let S be the set of all cars and R be “is the same color as”. Then R partitions S into mutually disjoint equivalence classes of cars of the same color (red, blue, green, black, brown, etc).

2) Let S be the set of all people and R be “is the same age as”. Then R partitions all people into mutually disjoint equivalence classes of people of the same age.

3) Let S be the set of all people and R be “is the same sex as”. Then R partitions all people into two mutually disjoint equivalence classes of people of the same sex.

4) Let S be the set of all people and R be “is the same race as”. Then R partitions all people into mutually disjoint equivalence classes of people of the same race.

5) Let S be the set of all triangles and R be “congruence”. Then R partitions all triangles into mutually disjoint equivalence classes of congruent triangles.

Other examples of equivalence classes:

6) the mutually disjoint classes of triangles induced by the relation of similarity for triangles

7) the residue classes of integers mod n

8) the mutually disjoint classes of matrices induced by the relations of equivalence, similarity, or congruence for matrices

Quotient set. If A₁, A₂, A₃, ... represent the equivalence classes (the disjoint subsets) into which a set S is partitioned by a relation R then

S/R = {A₁, A₂, A₃, ... }

is called the quotient set. Thus the quotient set S/R is a set of sets since A₁, A₂, A₃, ... are sets.

***********************************************************************

Open sentences. The most general case of an open sentence in two variables is one in which the two variables are from two different sets A and B.

Example 1. Let A be the set of all authors and B be the set of all books. Then “x wrote y” constitutes an open sentence involving members of two sets.

Example 2. Let A be the set of all people and B be the set of all countries. Then the open sentence “x lives in y” involves members of two sets.

Def. Truth set of an open sentence. Let S(x, y) denote an open sentence on two sets A and B in which x ε A and y ε B. Then S(x, y) partitions the Cartesian product A B into two mutually disjoint subsets, one subset consisting of all pairs (x, y) for which S(x, y) is true, the other subset consisting of all pairs (x, y) for which the relation S(x, y) is false. That subset of A B for which S(x, y) is true is called the truth set of S(x, y).

A relation relates two members of a single set P. A relation xRy is a special case of an open sentence. Generally, an open sentence of the form xRy states some relation relating two members x and y of a single set P.

Examples.

1) “x is parallel to y” where P is the set of all lines in the plane

2) “x is the uncle of y” where P is the set of all people in Chicago

3) “x divides y” where P is the set of all positive integers

4) “x is congruent to y” where P is the set of all triangles in the plane

Def. Truth set of a relation. Let xRy be an open sentence in which x and y are members of set P. Then R partitions the Cartesian product P P into two mutually disjoint subsets, one subset consisting of all pairs (x, y) for which xRy is true, the other subset consisting of all pairs (x, y) for which the relation xRy is false. That subset of P P for which xRy is true is called the truth set of xRy.

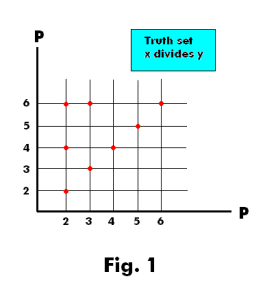
Example 1. Consider the open sentence “x divides y” where x and y are members of set

P = {2, 3, 4, 5, 6}

The truth set is the set

T = {(2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}

This truth set can be represented graphically as is done in Fig. 1. The truth set corresponds to the red dots in the figure. Corresponding to each member of P (i.e. the numbers 2, 3, 4, 5, 6) listed along the horizontal axis is plotted, on the vertical line, those members of P that satisfy the relation.

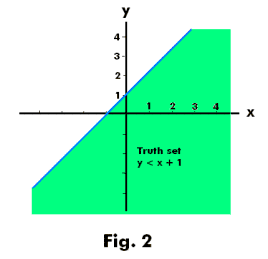
Example 2. Consider the open sentence “y < x + 1” where x and y are members of the set R^# of real numbers. The truth set is shown in Fig. 2.

Comments. After defining a relation as we have done above, most authors now redefine a relation as the truth set of the relation i.e. they define a relation R as being that set of ordered pairs (x, y) in P P for which the relation is valid. I am unwilling to do this. A relation is not a set. A relation and a set are two completely different animals. To do this is to just cause confusion and muddy the waters. The notion of a relation is just too different from the concept of a set of objects. Someone might say, “We call a number triplet (a, b, c) a point or a vector so why can’t we call a relation a set?” Well, we need to reserve the term “relation” for the ordinary concept of a relation and call something completely different by another name.

References

Lipschutz. Set Theory. (Schaum)

James & James. Mathematics Dictionary

Burington. Handbook of Mathematical Tables and Formulas

Ayres. Modern Algebra. (Schaum)