Website owner: James Miller
Solution of linear differential equations by power series. Solutions about ordinary points and singular points.
Introduction. Not every differential equation can be solved — a solution may not exist. There may be no function that satisfies the differential equation. If a solution does exist it may not be possible to express it in closed form in terms of the elementary functions familiar from calculus (i.e. the algebraic, trigonometric, exponential, etc. functions). There are differential equations of great importance in higher mathematics and engineering that cannot be solved in terms of elementary functions. In such cases one must turn to approximate methods such as power series. The solutions to many differential equations are expressible in terms of a power series of the form
1) y = a0 + a1x + a2x2 + a3x3 + ....... .
We will now consider methods for finding solutions in terms of a power series. We remark, however, that an equation may be solvable but yet not solvable in terms of a series of the form 1). In such a case we must seek a solution in some other form. One such form is
2) y = xc(a0 + a1x + a2x2 + a3x3 + ....... )
which is a generalization of 1), since 2) gives 1) when c = 0. For example, if a particular differential equation had the solution
![]()
an assumption of a solution of type 1) would not give the solution but an assumption of a solution of type 2) would give it since 3) is a special case of 2) with c = 1/2, a0 = a1 = .... = 1. A series of type 2) is called a Frobenius type series.
Solution of linear equations by power series
Def. Ordinary point, singular point. Given a linear differential equation with polynomial coefficients
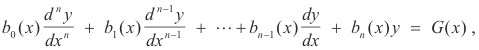
a point x = x0 is called an ordinary point if b0(x0)
![]() 0. If b0(x0) = 0 the point is called a
singular point.
0. If b0(x0) = 0 the point is called a
singular point.
Theorem 1. Let x = 0 be an ordinary point of the linear equation
1) b0(x)y" + b1(x)y' + b2(x)y = 0
with polynomial coefficients. Then there is a solution of the form
2) y = a0 + a1x + a2x2 + a3x3 + .......
containing two arbitrary coefficients a0 and a1 which converges inside a circle with center at x = 0 that extends out to the nearest singular point. Solution 2) is a solution of 1) but it is not the only solution. The complete solution of 1) is given in the following theorem:
Theorem 2. Let x = 0 be an ordinary point of the linear equation
1) b0(x)y" + b1(x)y' + b2(x)y = 0
with polynomial coefficients. Then this equation can be solved in series about point x = 0 as
3) y = A{series in x} + B{series in x}
in which A and B are arbitrary constants and the two “series in x” are two different series to be determined. The two series are linearly independent and both are convergent in a region surrounding x = 0.
The solution 3) is the complete solution of 1).
Theorem 3. The complete solution of the linear equation
4) b0(x)y" + b1(x)y' + b2(x)y = G(x)
consists of its complementary function plus any particular solution. The complementary function of 4) consists of the complete solution of the homogeneous equation
b0(x)y" + b1(x)y' + b2(x)y = 0
**********************************************************************
**********************************************************************
Methods of solution
Method of Undetermined Coefficients. The Method of Undetermined Coefficients is the most common method of solving a differential equation by power series. Suppose we wish to solve the equation with polynomial coefficients
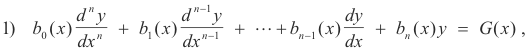
about an ordinary point x = 0 using a power series. We proceed as follows:
Step 1. Assume a solution of the form
2) y = a0 + a1x + a2x2 + a3x3 + .......
where a0, a1, .... ,an-1 are arbitrary constants and the remaining a’s are constants to be determined.
Step 2. Substitute the assumed series 2) into the differential equation 1). This substitution will yield an equation of form
3) A0(a0, a1, a3, ... ) + A1(a0, a1, a3 ... ) x + A2(a0, a1, a3 ... ) x2 + A3(a0, a1, a3 ... ) x3 + .......
![]() 0
0
This equation represents an identity and for this power series to vanish identically over any interval each coefficient must be zero. Thus
A0( a0, a1, a3 ... ) = 0
A1(a0, a1, a3 . .. ) = 0
4) A2(a0, a1, a3 ... ) = 0
..............................
..............................
An(a0, a1, a3 ... ) = 0
..............................
Step 3. From equations 4) we can compute the values of the a’s. We will now give an example that will clarify details of the procedure.
Technique for finding solutions near an ordinary point by the Method of Undetermined Coefficients.
Problem 1. Solve the equation
1) (1 - x2)y" - 6xy' - 4y = 0
near the ordinary point x = 0.
Solution. This equation has singular points at x = 1 and x = -1. Thus there will be a solution
2) y = a0 + a1x + a2x2 + a3x3 + .......
valid for |x| < 1.
Step 1. Obtain basic equation. We wish to write down the equation that is obtained when 2) is substituted into 1). We can do this by inspection. Simply apply 1) to the general term anxn of 2) i.e substitute the general term anxn of 2) into 1).
Let us write 1) as
3) y" - x2y" - 6xy' - 4y = 0
Then substitution of anxn into 3) gives
y"
![]() n(n - 1)anxn -2
n(n - 1)anxn -2
x2y"
![]() n(n - 1)anxn
n(n - 1)anxn
6xy'
![]() 6nanxn
6nanxn
4y
![]() 4anxn
4anxn
The equation obtained by substituting 2) into 1) is then
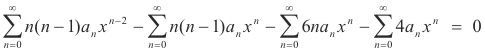
Combining terms we get
![]()
We now factor the coefficient in the second series to get
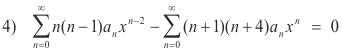
Step 2. Do index shift. We wish now to do an index shift on 4). We wish to alter 4) into an equivalent equation through a device called an index shift. The object of the index shift is to make the exponents of x in both series the same.
We now shift the index in the second series by replacing n everywhere with (n - 2). The n = 0 in the summation sign then becomes n - 2 = 0, or n = 2. With this index shift 4) becomes
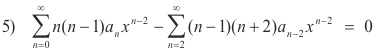
We now note that the equation
![]()
corresponds to the equation
An(a0, a1, a3 ... ) = 0
discussed above. Equation 5) represents an identity and in order the series to vanish identically the coefficients in the series must be zero.
Step 3. Get recurrence relation. Let us now write out 6) for different values of n. For n = 0 and n = 1 the second series has not yet started and we get contributions only from the first series.
We have
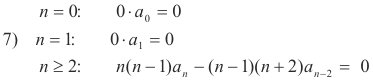
As expected, we see that a0 and a1 are arbitrary. We can rewrite the last equation above as
![]()
Equation 8) is called a recurrence relation. It gives an in terms of preceding a’s. In this particular case each a is determined by the a with a subscript two lower than its own. Thus all the a’s are ultimately expressible in terms of either a0 or a1 according to whether the a has an even or odd subscript.
Step 4. Set up columns and use multiplication device to obtain an expression for the a’s. We now obtain expressions for the values of the a’s utilizing a multiplication device that we shall shortly explain.
Let us list the iterated instances of 8) in two columns (two columns because the subscripts in 8) differ by two) listing n = 2, 4, 6, .... in the first column and n = 3, 5, 7, .... in the second column.
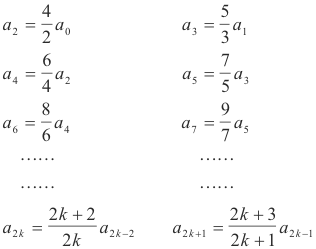
We now employ our multiplication device on the first column to obtain an expression for a2k. The device consists simply of this: Multiply all equations of the column together and then perform cancellations and simplifications on the result. Multiplying the equations together we get
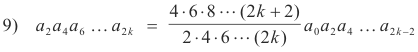
Cancellation and simplification in 9) gives
10) a2k = (k + 1)a0 k = 1, 2, 3, ....
We now do the same thing with the second column. Multiplying the equations together we get

which, on simplification, gives
![]()
![]()
Step 5. Substitute the expressions for the coefficients into the assumed series 2) to obtain the solution. We now substitute the expressions for the coefficients into series 2). Because of the nature of the expressions for the a’s the final solution will be written as the sum of two series, one with even subscripts and the other with odd subscripts. The solution will be of the form
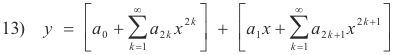
Substituting the values of a2k and a2k+1 into 13) we get as the general solution
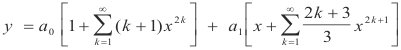
In this example the equation was homogeneous and of second order. Raising the order introduces nothing except additional labor. A nonhomogeneous equation with right member G(x) that is an analytic function is no worse to handle than a homogeneous equation.
Problem 2. Solve the equation
1) y" + (x - 1)2y' - 4(x - 1)y = 0
about the ordinary point x = 1.
Solution. To solve an equation about a point x = a means to obtain a solution valid in a region surrounding the point a with the solution expressed in powers of (x - a).
We first translate the axes, setting x - 1 = v. Thus when v = 0, x = 1. With this translation 1) becomes
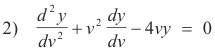
In a pure translation, x - a = v, the following holds
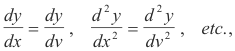
a relevant fact in transforming 1) into 2).
We now solve 2) about point v = 0.
As usual we assume a solution
3) y = a0 + a1v + a2v2 + a3v3 + ....... .
The equation obtained by substituting 3) into 2) is
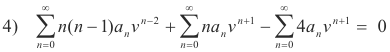
[obtained by inspection by substituting the general term anvn of 3) into 2)].
Collecting like terms we get
![]()
We now do a shift of index from n to (n - 3) in the second series to obtain
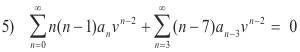
We now give the expressions for the coefficients:
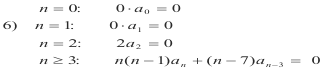
or
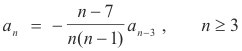
which is the recurrence relation.
a0 and a1 are arbitrary constants and a2 = 0.
The a’s fall into three groups, those coming from a0, those coming from a1 and those coming from a2. We use three columns:
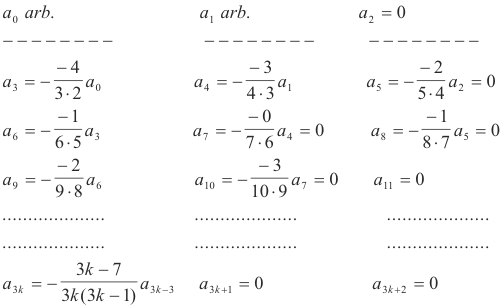
Using our multiplication device we multiply the equations of the first column together and obtain
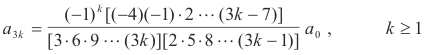
As for the a’s that are determined by a1, we note that a4 = a1/4 and all the rest are zero. Since a2 = 0, all a’s determined by it are zero.
We thus have for y
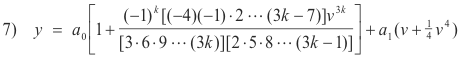
Substituting v = x - 1 into 7) we obtain the general solution of 1):
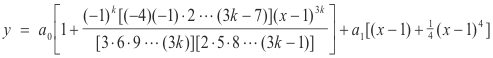
Summary of procedure. Ordinary point.
1. Assume a solution of the form
y = a0 + a1x + a2x2 + a3x3 + .......
2. Substitute assumed solution into differential equation to get basic equation L(y) = 0.
3. Collect in like powers of x
4. Shift index
6. Derive recurrence relation.
7. Set up columns and use multiplication devise to obtain an. Choose a0 = 1.
8. Write solution.
***********************************************************************
Regular and irregular singular points. Let x = x0 be a singular point of the equation
1) b0(x)y" + b1(x)y' + b2(x)y = 0
with polynomial coefficients. Then b0(x0) = 0, which implies that b0(x0) has a factor (x - x0) to some power. Let us now divide 1) by b0(x), putting 1) into the form
2) y" + p(x)y' + q(x)y = 0
where p(x) = b1(x)/b0(x) and q(x) = b2(x)/b0(x). Here p(x) and q(x) are rational functions where at least one and possibly both have denominators containing the factor (x - x0). If the denominator of p(x) does not contain the factor (x - x0) to a power higher than one, and if the denominator of q(x) does not contain the factor (x - x0) to a power higher than two, then x = x0 is called a regular singular point of 1). If a singular point is not a regular singular point it is called an irregular singular point.
Singular points of equations of higher order are classified in a similar way. For example, the singular point x = x0 of the equation
3) y"' + p1(x)y" + p2(x)y' + p3(x)y = 0
is called regular if the factor (x - x0) does not appear in the denominator of p1(x) to a power higher than one, of p2(x) to a power higher than two and of p3(x) to a power higher than three. If the singular point is not regular, it is called irregular.
Example 1. Classify the singular points, in the finite plane, of the equation
x4(x2 + 1)(x - 3)y" + x3y' + (x + 1)y = 0
Solution. We have
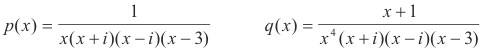
The regular singular points are at x = i, -i, 3. The irregular singular points are at x = 0.
Theorem 4. If x = a is a regular singular point of the differential equation
b0(x)y" + b1(x)y' + b2(x)y = 0
a solution of the form
4) y = (x - a)c [a0 + a1(x - a) + a2(x - a)2 + a3(x - a)3 + ....... ]
always exists.
If x = a is an irregular singular point, solutions of the form 4) may or may not exist.
We will deal with the problem of finding solutions near regular singular points. The problem of finding solutions near irregular singular points is substantially more difficult and we won’t deal with it.
Technique for finding solutions in the vicinity of a regular singular point by the Method of Undetermined Coefficients.
We will consider the problem of finding solutions of the equation
1) b0(x)y" + b1(x)y' + b2(x)y = 0
about a singular point x = 0. If we wish to obtain a solution about a point x = a, we first translate the origin to that point by a change of variable. We thus reduce the problem of finding a solution about a point x = a to one of finding a solution about the point x = 0.
Let us denote the left member of 1) by
L(y) = b0(x)y" + b1(x)y' + b2(x)y .
We will find the notation useful in referring to the left member.
Solving equation 1) in the vicinity of a regular singular point involves solving an equation called an indicial equation that arises at a certain point in the procedure. Once we have the roots of the indicial equation subsequent procedure depends on the nature of the roots of the indicial equation.
We will now outline of the procedure up to the point where we obtain the indicial equation. The procedure after that is best explained by example.
Step 1. Assume solution. Assume a solution of the form
2) y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
where a0
![]() 0.
0.
Step 2. Substitute assumed solution into differential equation. Substitute the assumed series 2) into the differential equation 1), collect like terms, and do an index shift in such a way as to bring all the exponents of x down to the smallest one present. This will yield an equation of form
3) L(x) = A0(c, a0 )xm + A1(c, a0, a1) xm+1 + A2(a0, a1, a3 ... ) xm+2 + A3(a0, a1, a3 ... ) xm+3 +
.......
![]() 0
0
This equation is an identity and because of that all of the coefficients A0(c, a0 ), A1(c, a0, a1), A2(a0, a1, a3 ... ), ....... must vanish.
Step 3. Compute roots of indicial equation. The coefficient of the lowest power of x, A0(c, a0 ), will be of the form
A0(c, a0 ) = f(c)a0
where f(c) is an algebraic expression of the second degree in c. Because 3) is an identity this
coefficient must vanish. Since a0
![]() 0, the only way for it to vanish is for f(c) to be zero. Thus
the coefficient A0(c, a0 ) will vanish only at those values of c for which f(c) = 0. The equation
0, the only way for it to vanish is for f(c) to be zero. Thus
the coefficient A0(c, a0 ) will vanish only at those values of c for which f(c) = 0. The equation
4) f(c) = 0
is called the indicial equation. So we now compute its roots c1 and c2. Solutions of our equation will only occur at those values of c.
***********************************************************************
Theorem 5. Let x = 0 be a regular singular point of the equation
1) y" + p(x)y' + q(x)y = 0
where p and q are rational functions of x. Let
r(x) = xP(x)
s(x) = x2Q(x)
Now let
a = r(0)
b = s(0)
i.e. the values of r(x) and s(x) at x = 0. Then the indicial equation is given by
c2 + (a - 1)c + b = 0
Theorem 6. Let x = 0 be a regular singular point of the equation
b0(x)y" + b1(x)y' + b2(x)y = 0 .
Then the equation has a general solution either of the form
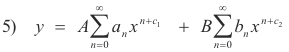
or of the form
![]()
where c1 and c2 are roots of the indicial equation and A and B are arbitrary constants.
The infinite series that occur in the above general solutions converge in at least the annular region of the complex plane bounded by two circles centered at x = 0, one of arbitrarily small radius, the other extending to the singular point nearest x = 0.
The form of the general solution of the equation depends on the nature of the roots c1 and c2 of the indicial equation according to the following three cases:
Case 1. The roots c1 and c2 are distinct and the difference c2 - c1 is not an integer. The general solution is of the form
y = Ay1 + By2
where A and B are arbitrary constants and y1 and y2 are particular solutions given by
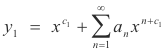
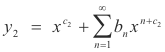
The ai coefficients are determined by substituting c = c1 into the recurrence relation and the bi coefficients are determined by substituting c = c2 into the recurrence relation.
Case 2. The roots c1 and c2 are equal. The general solution is of the form
y = Ay1 + By2
where A and B are arbitrary constants and y1 and y2 are particular solutions given by
![]()
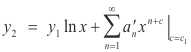
where the variable c in the a’s is carried through to the end,
a'n = ∂an /∂c,
and y1 and y2 are evaluated at c = c1 = c2.
Case 3. The roots c1 and c2 are distinct and the difference c2 - c1 is an integer. The general solution may be of the general form
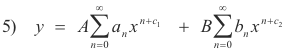
or of the form
![]()
depending on the equation.
***********************************************************************
Case 1. Roots of indicial equation differ by non-integer.
Problem. Solve the equation
1) 2xy" + (1 + x)y' - 2y = 0
about the point x = 0.
Solution. This equation has a regular singular point at x = 0.
Step 1. Assume solution. Assume a solution of the form
2) y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
where a0
![]() 0.
0.
Step 2. Substitute assumed solution into differential equation. Substitute the assumed series 2) into the differential equation 1), collect like terms, and do an index shift in such a way as to bring all the exponents of x down to the smallest one present.
Substitution of 2) into 1) gives
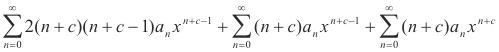
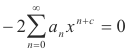
or
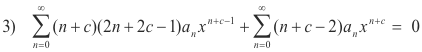
We now shift the index to bring all exponents down to the smallest one present by replacing all n’s in the second summation by (n -1)
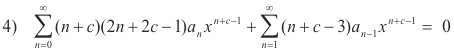
Step 3. Compute roots of indicial equation. The total coefficient of each power of x in 4) must vanish. The equations for determining c and the a’s are
5) n = 0: c(2c - 1)a0 = 0
n
![]() 1: (n + c)(2n + 2c - 1)an + (n + c - 3)an-1 = 0
1: (n + c)(2n + 2c - 1)an + (n + c - 3)an-1 = 0
The indicial equation is then given by
c(2c - 1) = 0
Its roots are c1 = 0 and c2 = 1/2. At these values of c and only at these values will solutions to the equation exist since only at these values will the n = 0 coefficient be zero. We note that the difference c2 - c1 is not an integer. We are thus dealing with the nonintegral case. In this case our method will always give two linearly independent solutions of the form 2), one for each root of c.
Computation of solution corresponding to the first root.
Step 4. Derive recurrence relation for first root. We will do the root c = 1/2 first. Substituting c = 1/2 into the second equation of 5) we obtain
(n + 1/2)(2n + 1 - 1)an + (n + 1/2 - 3)an-1 = 0 n
![]() 1
1
which gives the recurrence relation
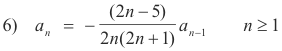
Step 5. Set up column and use multiplication devise to obtain an. Substituting into 6) we get, for different values of n
a0 arbitrary
-------------
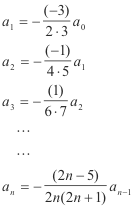
Multiplying these equations together and simplifying we get
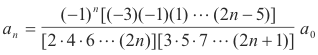
which can be simplified to
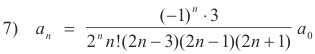
Step 6. Write solution. Using a0 = 1, the an from 7) and c = 1/2, the solution is given by
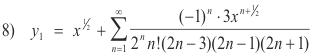
Computation of solution corresponding to the second root.
In computing the solution for the second root it is obvious that the a’s will be different from those of the first root. To avoid confusion let us therefore change notation and use b’s in place of a’s.
Step 7. Derive recurrence relation for second root. Substituting c = 0 into the second equation of 5) we obtain
(n)(2n- 1)bn + (n - 3)bn-1 = 0 n
![]() 1
1
which gives the recurrence relation
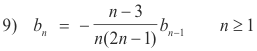
Step 8. Set up column and use multiplication devise to obtain bn. Substituting into 9) we get, for different values of n
b0 arbitrary
-------------
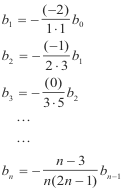
We note that b3 and all subsequent b’s are zero. Using b0 = 1, we obtain for b1 and b2
b1 = 2
b2 = 1/3
The second solution is then
![]()
The solutions we have derived, y1 and y2, are linearly independent particular solutions to the equation and the general solution is given by
y = Ay1 + By2
Summary of procedure. Difference of indicial roots a non-integer.
1. Assume a solution of the form
y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
2. Substitute assumed solution into differential equation to get basic equation L(y) = 0.
3. Collect in like powers of x
4. Shift index
5. Compute roots of indicial equation.
6. Derive recurrence relation using first root.
7. Set up column and use multiplication devise to obtain an(c). Choose a0 = 1.
8. Write solution.
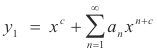
9. Repeat steps 6 - 8 using second root to obtain second solution y2.
10. General solution is
y = Ay1 + By2
where A and B are arbitrary constants
********************************************************************
Case 2. Roots of indicial equation equal.
Problem. Solve the equation
1) x2y" + 3xy' + (1 - 2x)y = 0
about the point x = 0.
Solution. This equation has a regular singular point at x = 0.
Step 1. Assume solution. Assume a solution of the form
2) y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
where a0
![]() 0.
0.
Step 2. Substitute assumed solution into differential equation. Substitute the assumed series 2) into the differential equation 1), collect like terms, and do an index shift in such a way as to bring all the exponents of x down to the smallest one present.
Substitution of 2) into 1) gives
![]()
or
![]()
or
![]()
We now shift the index to bring all exponents down to the smallest one present by replacing all n’s in the second summation by (n -1)
![]()
Step 3. Compute roots of indicial equation. The coefficient of the lowest power of x, A0(c, a0 ), n = 0, is
A0(c, a0 ) = (c+1)2a0
and so the indicial equation is
(c+1)2 = 0 .
The roots of the indicial equation are c1 = -1, c2 = -1. We thus have the case of equal indicial roots. Now we know that the general solution of our differential equation consists of a linear combination of two linearly independent particular solutions. Using the method of the previous case we can get from two equal roots only one particular solution. By what method might we obtain another linearly independent solution? Luckily someone has discovered a method. We proceed as follows.
1. We refrain from choosing a value for c for the present and remove, for the present, the requirement that the function L(y) equal zero.
2. We set equal to zero all the coefficients Ai(c, a0, a1, ... ) of the various powers of x in 4) except for the A0(c, a0 ) coefficient of the n = 0 term.
With what we have done the function L(y) of 4) reduces to a single term, the A0(c, a0 ), n = 0, term i.e.
5) L(y) = (c+1)2a0xc
Step 4. Derive recurrence relation. We now derive the recurrence relation retaining the
variable c in the relation. For n
![]() 1 we have
1 we have
(n + c + 1)2an - 2an -1 = 0 n
![]() 1
1
or
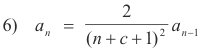
Step 5. Set up column and use multiplication devise to obtain an. Substituting into 6) we get, for different values of n
a0 arbitrary
-------------
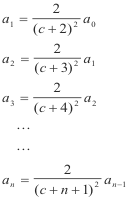
Multiplying these equations together and simplifying we get
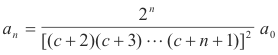
Step 6. Write function y(x, c). To obtain a particular solution we choose a0 = 1 and, from these a’s, write down the function y(x, c):
![]()
where
![]()
Now by 5) above
9) L[y(x, c)] = (c+1)2xc
A solution of the original differential equation is a function y for which L(y) = 0. We note that a choice of c = -1 yields a solution since it makes the right member of 9) zero.
Let us now take the partial derivative of both sides of 9) with respect to c. We get
![]()
We make the observation that the value c = -1 will also reduce the right side of this equation to zero. Might ∂ L[y(x, c)] / ∂c provide us with that second linearly independent solution that we desire? Indeed it will. We now make the following observation. The factor (c + 1) occurs squared in 9) and the fact that it is squared is an automatic consequence of the equality of the roots of the indicial equation. Thus whenever we have two equal indicial roots we can expect this squared factor. Moreover we know from calculus that when a function contains a factor to a certain power the derivative of that function contains the same factor to a power one lower than the original. Thus we can expect ∂ L[y(x, c)] / ∂c to provide us with a second solution whenever the indicial roots are equal. It can be shown that
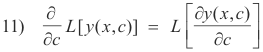
As a consequence of all this it can be seen that two solutions of the equation L(y) = 0 are
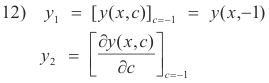
We have y(x, c) from 7) and we need ∂y(x, c) /∂c. Taking the partial derivative with respect to c of 7) we get
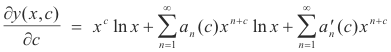
which simplifies to
![]()
where
![]()
The solutions y1 and y2 will be obtained by putting c = -1 in equations 7) and 13) i.e. they are given by
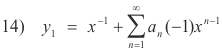
![]()
Thus we need to evaluate an(c) and an'(c) at c = -1. We know that
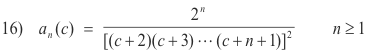
The following theorems are often useful in evaluating an'(c).
Theorem 7. Let
![]()
where each of the u’s is a function of x. Let differentiation with respect to x be denoted by primes. Then
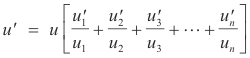
Theorem 8. Let
![]()
Then
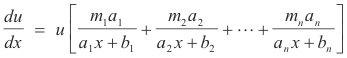
Writing 16) as
an(c) = 2n [(c + 2)-1 (c + 3)-1 ....... (c + n + 1)-1] [ (c + 2)-1 (c + 3)-1 ....... (c + n + 1)-1]
and applying Theorem 8 we get
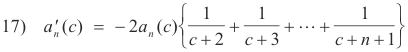
Substituting c = -1 into 16) gives
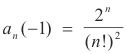
and
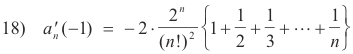
A frequently used notation for the partial sum of a harmonic series is
![]()
Using this notation 18) can be written more simply as
![]()
The desired solutions are then
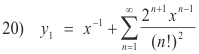
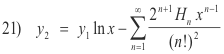
The general solution, valid for all finite x
![]() 0, is given by
0, is given by
y = Ay1 + By2
where A and B are arbitrary constants.
Summary of procedure for equal roots.
1. Assume a solution of the form
y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
2. Substitute assumed solution into differential equation to get basic equation L(y) = 0.
3. Collect in like powers of x
4. Shift index
5. Compute roots of indicial equation.
6. Derive recurrence relation
7. Set up column and use multiplication devise to obtain an(c). Choose a0 = 1.
8. Derive expression for an'(c) from an(c)
9. Solutions are given by
![]()
![]()
********************************************************************
Case 3. Difference of indicial roots an integer. Non-logarithmic case.
Problem. Solve the equation
1) xy" - (4 + x)y' + 2y = 0
about the point x = 0.
Solution. This equation has a regular singular point at x = 0.
Step 1. Assume solution. Assume a solution of the form
2) y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
where a0
![]() 0.
0.
Step 2. Substitute assumed solution into differential equation. Substitute the assumed series 2) into the differential equation 1), collect like terms, and do an index shift in such a way as to bring all the exponents of x down to the smallest one present.
Substitution of 2) into 1) gives
![]()
or
![]()
Step 3. Compute roots of indicial equation. The coefficient of the lowest power of x, A0(c, a0 ), n = 0, is
A0(c, a0 ) = c(c - 5)a0
and so the indicial equation is
c(c - 5) = 0 .
The roots of the indicial equation are c1 = 0, c2 = 5. Thus we are dealing with the case where the difference between indicial roots is an integer. In this case the solution may include a logarithm or it may not. We don’t yet know. The two type solutions are handled differently. We don’t currently know which we are dealing with. To find out whether we need to use the non-logarithmic or logarithmic procedure we proceed as follows: Let s = c2 - c1, where c2 is the larger of the roots, making s positive. It may be possible to obtain two power series solutions, one starting with an x0 term and the other starting with an xs term. If it happens that both a0 and as turn out to be arbitrary we can obtain the general solution by this method. Otherwise we must use the logarithmic procedure. If both a0 and as are arbitrary we assume a solution of the form 2) above and use the smaller root i.e.c1. The series we get will then include both solutions.
Step 4. Choose smallest root, c1. Write out the relation for the coefficients up through n = , c2 - c1 substituting in the smallest root, c1, for the variable c. Write recurrence relation. Substituting c = c1 = 0 into 3) above gives
![]()
The relationships for the coefficients are
n = 0; 0·a0 = 0 (a0 arbitrary)
n
![]() 1: n(n - 5)an - (n - 3)an -1 = 0
1: n(n - 5)an - (n - 3)an -1 = 0
Because division by (n - 5) cannot be accomplished until n > 5, we write the relationships out explicitly through the critical one for a5.
n = 1: -4a1 + 2a0 = 0
n = 2: -6a2 + a1 = 0
n = 3: -6a3 + 0·a2 = 0
n = 4: -4a4 - a3 = 0
n = 5: 0·a5 - 2a4 = 0
Recurrence relation:
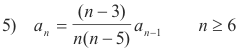
From the above relationships we derive
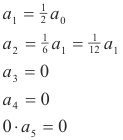
Thus we see that a5 is arbitrary and we can use the non-logarithmic method. The an for n > 5 will be obtained in the usual way.
Step 5. Set up column and use multiplication devise to obtain an. Substituting into 5) we get, for different values of n
a5 arbitrary
-------------
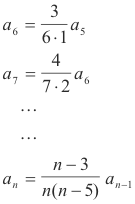
Multiplying these equations together and simplifying we get
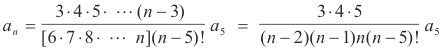
The general solution is then
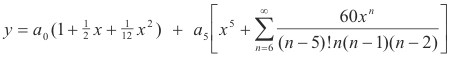
where a0 and a5 are arbitrary constants.
********************************************************************
Case 4. Difference of indicial roots an integer. Logarithmic case.
Problem. Solve the equation
1) x2y" + x(1 - x)y' - (1 + 3x)y = 0
about the point x = 0.
Solution. This equation has a regular singular point at x = 0.
Step 1. Assume solution. Assume a solution of the form
2) y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
where a0
![]() 0.
0.
Step 2. Substitute assumed solution into differential equation. Substitute the assumed series 2) into the differential equation 1), collect like terms, and do an index shift in such a way as to bring all the exponents of x down to the smallest one present.
Substitution of 2) into 1) gives
![]()
Doing an index shift gives
![]()
Step 3. Compute roots of indicial equation. The coefficient of the lowest power of x, A0(c, a0 ), n = 0, is
A0(c, a0 ) = (c + 1)(c - 1)a0
and so the indicial equation is
(c + 1)(c - 1) = 0.
The roots of the indicial equation are c1 = -1, c2 = 1. This represents a case where the difference
between indicial roots is an integer. The solution may involve a logarithm or it may not. We
don’t yet know. However, we note that there is no power series solution that starts with
![]() and
so we suspect the presence of a logarithmic term.
and
so we suspect the presence of a logarithmic term.
Step 4. Choose smallest root, c1. Write out the relation for the coefficients up through n = c2 - c1 , substituting in the smallest root, c1, for the variable c. Write recurrence relation. Substituting c = c1 = -1 into 3) above gives
![]()
The relationships for the coefficients are
n = 0; 0·a0 - a-1 = 0
n
![]() 1: n(n - 2)an - (n + 1)an -1 = 0
1: n(n - 2)an - (n + 1)an -1 = 0
n = 1: -a1 - 2a0 = 0
n = 2: 0 · a2 - 3a1 = 0
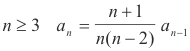
From the above we derive
a1 = -2a0
0 · a2 = 3a1 = -6a0
The only way these relationships could be satisfied is by choosing a0 = 0. And if we did that a2 would be the only arbitrary constant. We would only get a single solution, that corresponding to the large value of c, c2 = 1. A logarithmic solution is indicated.
We now proceed in the same manner that we did in obtaining a logarithmic solution for the case of equal roots:
1. We refrain from choosing a value for c for the present and remove, for the present, the requirement that the function L(y) equal zero.
2. We set equal to zero all the coefficients Ai(c, a0, a1, ... ) of the various powers of x in 3) except for the A0(c, a0 ) coefficient of the n = 0 term.
With what we have done the function L(y) of 3) reduces to a single term, the A0(c, a0 ), n = 0, term.
We now write from 3) the recurrence relation, retaining the variable c.
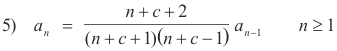
Step 5. Set up column and use multiplication devise to obtain an. Substituting into 5) we get, for different values of n
a0 arbitrary
-------------
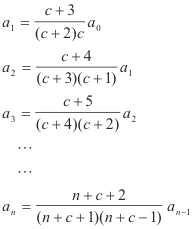
Multiplying these equations together and simplifying we get
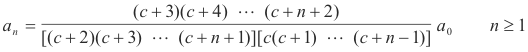
or
![]()
We now write down the function y(x, c):
![]()
or
![]()
Since all terms in the power series have been made to vanish this function y(x, c) must satisfy
8) L(y) = (c+1)(c-1)a0xc
Only one solution can be obtained from the larger root, c2 = 1. Two solutions could be obtained from the smaller root, c1 = -1, if the right member of 8) contained the factor (c + 1)2, instead of just (c + 1) to the first power. However, a0 is still arbitrary so if we were to take a0 = (c + 1) we would get the desired square in the right member of 8). This is what we do.
With a0 = (c + 1), 7) becomes
![]()
for which
L(y) = (c+1)2(c-1)xc
By the same argument that we used for the case of equal indicial roots we now assert that the following constitute two linearly independent solutions of our equation:
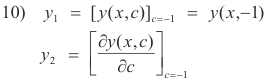
These solutions will have the form
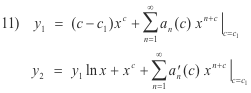
where c1 is the smaller indicial root and an(c) is given by
![]()
One should perform the cancellation of the factor (c + 1) from the numerator and denominator in the terms of the series in 9). However, the factor (c + 1) does not enter the denominator until the term n = 2. Thus it is best to write out the terms that far separately. We rewrite 9) as
![]()
Step 6. Derive an'(c). We now derive an'(c), n
![]() 1 utilizing Theorem 8 from the “Case 2,
Equal roots” section. Before obtaining an'(c), however, we must replace the factor a0 that an(c)
contains with the factor (c - c1) and perform any cancellations of this factor that may be possible
in some of the terms as we did in 13) above.
1 utilizing Theorem 8 from the “Case 2,
Equal roots” section. Before obtaining an'(c), however, we must replace the factor a0 that an(c)
contains with the factor (c - c1) and perform any cancellations of this factor that may be possible
in some of the terms as we did in 13) above.
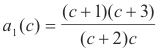
![]()
![]()
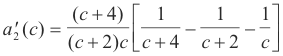
![]()
![]()
We are now in a position to evaluate y1 and y2 using 11) above at c = -1. Substituting into 11) and using the expressions for an'(c) that we have derived we obtain
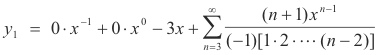
![]()
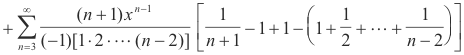
These results can be written more concisely as
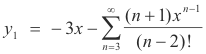
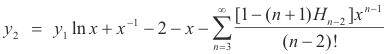
Summary of procedure for difference of indicial roots an integer. Logarithmic case.
1. Assume a solution of the form
y = xc[a0 + a1x + a2x2 + a3x3 + ....... ] = a0xc + a1xc+1 + a2xc+2 + a3xc+3 + .......
2. Substitute assumed solution into differential equation to get basic equation L(y) = 0.
3. Collect in like powers of x
4. Shift index
5. Compute roots of indicial equation.
6. Derive recurrence relation
7. Set up column and use multiplication devise to obtain an(c). Choose a0 = c - c1 where c1 is the smaller of the roots.
8. Replace the factor a0 that an(c) contains with the factor (c - c1) and perform any cancellations of this factor that may be possible in the various terms before deriving an'(c).
9. Derive expression for an'(c) from an(c)
10. Solutions are given by
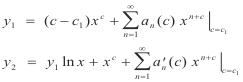
References
1. Murray R. Spiegel. Applied Differential Equations.
2. James B. Scarborough. Differential Equations and Applications.
3. Frank Ayres. Differential Equations (Schaum).
4. Earl Rainville. Elementary Differential Equations.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life