Website owner: James Miller
Methods for finding particular solutions of linear differential equations with constant coefficients. Method of Undetermined Coefficients, Variation of Parameters, Superposition. Operational methods.
We shall now consider techniques for solving the general (nonhomogeneous) linear differential equation with constant coefficients
![]()
The general solution is given by
y = yc + yp
where yc is the complementary function of 1) i.e. the general solution to the associated homogeneous equation
![]()
and yp is a particular solution. We already know how to obtain the complementary function yc so we will focus on techniques for obtaining a particular solution yp.
Methods for finding particular solutions
1. Method of Undetermined Coefficients. The Method of Undetermined Coefficients involves the skill of finding a homogeneous linear differential equation with constant coefficients when given its solution i.e. working backward from solution to equation. More specifically, we are given a particular solution to some homogeneous linear differential equation with constant coefficients and we want to know what the equation is. In that connection let us simply note the following facts:
● a single root m = a of the auxiliary equation f(x) = 0 gives rise to a term c1eax
● n repeated 0 roots, m = 0, 0, .... , 0 give rise to c1 + c2x + c3 x2 + ...... +cnxn -1
● the roots m = - i, i give rise to c1cos x + c2sin x
Problem. Find a homogeneous linear equation with constant coefficients which has as a particular solution
y = 3e4x + 2x2
Solution. A single root m = 4 will give rise to a term c1e4x. A triple 0 root m = 0, 0, 0 will give rise to a term c2x2. Thus the equation
D3(D - 4)y = 0
will contain a particular solution of the required form. Its general solution is
y = c1e4x + c2 + c3x + c4x2
and choice of c1 = 3, c2 = 0, c3 = 0 and c4 = 2 will give the particular solution
y = 3e4x + 2x2 .
Let us now consider the problem of finding a particular solution of the equation
2) D2(D - 1)y = 3ex + sin x
The roots of the auxiliary equation f(m) = 0 are
3) m = 0, 0, 1
and the complementary function is given by
4) yc = c1 + c2x + c3ex .
We wish to find a particular solution yp. The first step in the procedure is to find that homogeneous linear differential equation with constant coefficients which has as a particular solution the right-hand side of 2) i.e. the function G(x) = 3ex + sin x. It will be an equation whose auxiliary equation has the roots
6) m' = 1,
![]() i
i
which is the equation
7) (D - 1)(D2 + 1) y = 0
If now we multiply both sides of equation 2) by the differential operator (D - 1)(D2 + 1) we will annihilate the right member of 2) and obtain
8) (D - 1)(D2 + 1)D2(D - 1) y = 0
Any solution of 2) must satisfy 8) i.e. the solution set of 2) is a subset of the solution set of 8).
The general solution of 8) can be written down at once from the roots of its auxiliary equation,
those roots being the values m = 0, 0, 1 along with m' = 1,
![]() i . Thus the general solution is
i . Thus the general solution is
9) y = c1 + c2x + c3ex + c4xex + c5 cos x + c6 sin x
The general solution of 2) is
y = yc + yp
where
yc = c1 + c2x + c3ex .
The particular solution yp of 2) must then consist of at most the remaining terms in 9) i.e. it must be of the form
10) yp = Axex + B cos x + C sin x
It remains only to determine the values of the coefficients A, B, C by substitution of 10) into the original equation
2) D2(D - 1)y = 3ex + sin x .
Computing the coefficients. Computing derivatives we get
Dyp = A (xex + ex) - B sin x + C cos x
D2yp = A (xex + 2ex) - B sin x - C cos x
D3yp = A (xex + 3ex) + B sin x - C cos x
Substitution into 2) gives
11) Aex + (B + C) sin x + (B - C) cos x = 3ex + sin x
Since 11) is an identity and since ex, sin x and cos x are linearly independent, corresponding coefficients in the two members of 11) must be equal. Consequently
A = 3
B + C = 1
B - C = 0 .
Thus A = 3, B = 1/2, C = 1/2. Substituting into 10) we obtain the particular solution
![]()
The general solution is then given by
![]()
More detail on the underlying theory. Let us now consider the underlying theory of the above method in more detail. Consider the equation
12) f(D)y = G(x)
where f(D) is a polynomial in the operator D. Let the roots of the auxiliary equation be
13) m = m1, m2, ...... , mn .
The general solution of 12) is
14) y = yc + yp
where the complementary function yc can be obtained from the values of m and yp is a particular solution.
Now suppose that the right member G(x) of 12) is a particular solution of some homogeneous linear differential equation with constant coefficients,
15) h(D)y = 0 ,
whose auxiliary equation has the roots
![]()
The roots of the differential equation
17) h(D)f(D) y = 0
consist of the values of m from 13) and m' from 16). Because the roots include the values of m, the general solution of 17) contains the complementary function yc of equation 14). Thus it is of the form
y = yc + yq
Now, any particular solution of 12) must satisfy 17). If f(D)(yc + yq) = G(x), then f(D)yq = G(x) because f(D)(yc) = 0. Thus deleting yc from the general solution of 17) leaves a function yp which for some numerical values of its coefficients must satisfy 12), thus providing a particular solution yp for 12).
General remarks. The above method is applicable when, and only when, the right member of the equation is itself a particular solution of some homogeneous linear differential equation with constant coefficients. In general, it is applicable for the differential equation f(D)y = G(x) where G(x) contains a polynomial, terms of the form sin ax, cos ax, eax or combinations of sums and products of these (where a is a constant).
Outline of the general procedure
1. From the original equation f(D)y = G(x) find the values of m and m'
2. From the values of m and m' write yc and yp
3. Substitute the yp into f(D)y = G(x), equate corresponding coefficients, and compute the values of the coefficients
4. Write the general solution y = yc + yq
Source: Rainville. Elementary Differential Equations. p. 134 - 137
2. Method of Variation of Parameters. The Method of Variation of Parameters (also called the Method of Variation of Constants) is due to Lagrange and can be used to find a particular solution to any linear differential equation, whether the coefficients are constant or not, provided the complementary function has been found. Consider the equation
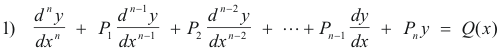
or, equivalently,
![]()
which has the complementary function
![]()
Lagrange showed that a particular solution to equation 1) can be obtained by a procedure in which the c’s in 3) are replaced by functions of x. We thus begin with the function
4) y = L1(x)y1 + L2(x)y2 + ......... + Ln(x)yn
formed by replacing the c’s of 3) by the L(x)’s. The method consists of determining the L’s in such a way that 4) satisfies 1). Relation 4) contains n unknown functions, L1, L2, ...... ,Ln to be determined. We have only one condition that must be satisfied ---- the condition that 4) satisfies the original equation 1). That gives us freedom to impose (n - 1) conditions which, with the differential equation, gives n conditions to determine the n unknown functions L1, L2, ...... ,Ln. We choose conditions that will make the determination of the L’s as simple and easy as possible.
A systematized procedure that utilizes the Method of Variation of Parameters is the following:
By differentiation of 4) we have
![]()
We now impose our first condition on the L’s:
![]()
So now 5) becomes
![]()
We now take the derivative of 7) to get
![]()
We now impose a second condition:
![]()
Equation 8) now becomes
![]()
We now take the derivative of 10) to get
![]()
We now impose a third condition:
![]()
Equation 11) now becomes
![]()
Continuing in this manner we finally arrive at
![]()
We now set our last condition. We set the quantity within the second parenthesis of 14) to Q(x):
![]()
Equation 14) now becomes
![]()
The conditions that we have imposed on the L’s form the following linear system of n equations
in the n variables
![]()
![]()
![]()
![]()
...............................................
...............................................
![]()
![]()
The determinant of this system is
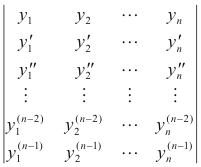
which is the Wronskian of y1, y2, ...... , yn. The determinant is not identically zero due to the assumption that the y’s are linearly independent. Thus the system of equations 17) can be solved for the L' ’s and the L’s can be found by integration.
We now show that 4) is a solution of 1) if the L’s satisfy 17). If we substitute the following equations
![]()
![]()
![]()
..........................................................................
..........................................................................
![]()
![]()
into 1) we obtain
![]()
![]()
or
L1 f(D) y1 + L2 f(D) y2 + ........ + Ln f(D) yn + Q(x) = Q(x)
or
0 + 0 + ......... + 0 + Q(x) = Q(x)
since y1, y2, ......, yn are solutions of F(D)y = 0.
3. Operational methods. Operational methods are those methods involving differential operators. The vast majority of linear differential equations with constant coefficients can be solved by the Method of Undetermined Coefficients. The rare equation that cannot be solved by this method can be solved by the Method of Variation of Parameters. There are, however, a large collection of methods that utilize differential operators. They sometimes give the solution with much less work than the two preceding methods. We will now consider some of them.
Inverse differential operators. Symbols of the form 1/f(D), where f(D) is a polynomial in D, are inverse differential operators.
Given the equation
1) f(D)y = g(x)
it is natural to wonder if an inverse of the operator f(D) might exist, an operator that would have the effect of undoing the action of f(D), thus enabling us to solve 1) for y by multiplying both sides by the inverse of f(D). Would it be possible to define such an inverse? If such an inverse could be defined, how might one define it? For insight, consider the simple equation
2) Dy = g(x)
How would an inverse D-1 = 1/D for this operation need to be defined? Since in this case we know that y is given by
![]()
it would need to correspond to the integration of a function i.e.
![]()
The symbol 1/D can be defined this way and is called an inverse operator. In the same way, an inverse operator 1/ D2 = (1/D)(1/D) can be defined which corresponds to double integration and an inverse operator 1/Dn can be defined that corresponds to n-fold integration.
Inverse operator 1/ (D - a). Let us now consider the equation
3) (D - a)y = g(x) .
What meaning might the inverse operator 1/ (D - a) have? Equation 3) has the solution
![]()
and so it is natural to interpret 1/(D- a) as
![]()
Ordinarily the inverse operator is employed only for finding particular integrals, in which case the arbitrary constant c is dropped and
![]()
Products of type (D - a)(D - b) ....... (D - q). Let us consider what we would expect the most natural meaning of
(D - a)(D - b)y
would be, where a and b are constants. We know that
![]()
The following would seem like a natural meaning:
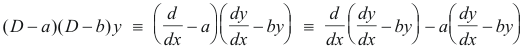
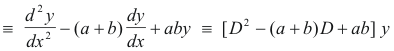
In fact, this is the meaning and we see that the operator (D - a)(D - b) is equivalent to D2 - (a + b)D + ab. The converse can also be established. It follows from this that operators with constant coefficients can be multiplied or factored like algebraic quantities.
Theorem. The operational factorization
a0Dn + a1Dn -1 + ........ + an
![]() a0(D - a)(D - b) ........ (D - q)
a0(D - a)(D - b) ........ (D - q)
is always possible and unique when a0, a1, .... , an, and consequently, a, b ..... q are constants.
Thus operators obey the commutative, associative and distributive laws in the same way algebraic quantities do. Because of this fact, we can introduce inverse operators of type
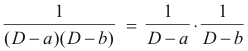
Using such an operator we can express the solution of the equation
(D - a)(D - b)y = g(y)
as
![]()
Using formula 5) we get
![]()
![]()
In a similar way we can write, for a case of n factors,
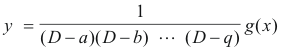
![]()
Solution by partial fractions. One might ask if one can resolve the inverse operator
![]()
into partial fractions in the same way we do algebraic fractions. The answer is yes. If
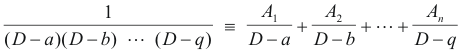
then
![]()
![]()
by 5).
*****************************************
Theorems
Theorem 1.
![]()
Theorem 2.
(D - a)n(xneax) = n!eax
Theorem 3.
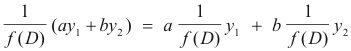
This shows that 1/f(D) is a linear operator.
Solution of the equation f(D)y = eax .
Case 1. f(a)
![]() 0. The solution of the equation f(D)y = eax is given by
0. The solution of the equation f(D)y = eax is given by
![]()
Case 2. f(a) = 0. If f(a) = 0, then f(D) contains the factor (D - a). Suppose a is an n-fold root and the factor occurs n times. Then
f(D) = g(D)(D - a)n
The solution then is
![]()
Note that formula 1) is contained in formula 2) as a special case , n = 0.
Problem. Solve (D2 - 2D - 3)y = e4x
Solution. Since f(4)
![]() 0, we have
0, we have
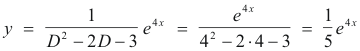
Solutions of equations of form f(D2) = sin (ax + b) and f(D2) = cos (ax + b). If the operator f(D) is a function of D2 as in f(D2) = D2 + 4 or f(D2) = D4 + 10D2 + 9 then
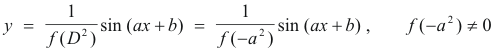
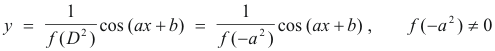
Example 1. Solve (D2 + 4)y = sin 3x
Solution. The complementary solution is y = c1 cos 2x + c2 sin 2x. A particular solution is
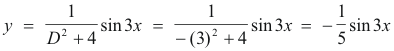
where we substitute -a2 for D2 in f(D).
Example 2. Solve (D4 + 10D2 + 9 )y = cos (2x + 3)
Solution. The complementary solution is y = c1 cos x + c2 sin x + c3 cos 3x + c4 sin 3x. A particular solution is
![]()
Source: Ayres. Differential Equations. p. 99,101
Operator-shift theorem. For a function g(x) and a constant a
![]()
or, equivalently,
![]()
This theorem shows how to shift an exponential factor from the right side of a differential operator to the left side.
Problem. Find a particular solution to (D2 - 2D + 1)y = xex
Solution.
(D2 - 2D + 1)y = xex
(D - 1)2y = xex
e-x (D - 1)2y = x
Using operator-shift we get
D2(e-xy) = x
![]()
![]()
Inverse operator-shift theorem.
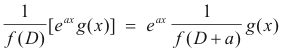
![]()
4. Miscellaneous methods
Method of superposition
Theorem. If y1 is a particular solution of f(D)y = G1(x) and y2 is a particular solution of f(D)y = G2(x) then
y = y1 + y2
is a particular solution of f(D)y = G1(x) + G2(x).
Thus it follows that the task of obtaining a particular solution of f(D)y = G(x) can be split up into parts by treating separate terms of G(x) independently.
This theorem follows directly from the linearity of a differential operator i.e
f(D)(c1f1 + c2f2) = c1 f(D)f1 + c2 f(D)f2
where c1 and c2 are constants and f1 and f2 are any functions of x.
Problem. Find a particular solution of (D2 - 9)y = 3ex + x
Solution. Since (D2 - 9)ex = -8ex, we see by inspection that
![]()
is a particular solution of (D2 - 9)y = 3ex . Similarly we see that y2 = -x/9 is a particular solution of (D2 - 9)y = x. Thus
![]()
Particular solution when G(x) is a constant. A particular solution of
![]()
where G(x) = G0, a constant, is as follows:
Case 1. an
![]() 0. The solution is yp = G0/an .
0. The solution is yp = G0/an .
Case 2. an = 0 and equation has the form (a0Dn + ........ + an-kDk)y = G0 where Dky is the lowest order derivative occurring. The solution is
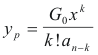
References
1. Max Morris / Orley Brown. Differential Equations.
2. James/James. Mathematics Dictionary.
3. Murray R. Spiegel. Applied Differential Equations.
4. James B. Scarborough. Differential Equations and Applications.
5. Frank Ayres. Differential Equations (Schaum).
6. Eshbach. Handbook of Engineering Fundamentals.
7. Earl Rainville. Elementary Differential Equations.
8. Harold Wayland. Differential Equations Applied in Science and Engineering.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life