Prove: Theorem. Let M(x, y), N(x, y), ∂M/∂y and ∂N/∂x be continuous functions of x and y. Then a necessary and sufficient condition that the differential equation

1)        M(x, y) dx + N(x, y) dy = 0

be exact is

Proof.

Part 1. We first prove that if 1) is exact then necessarily ∂M/∂y = ∂N/∂x. If 1) is exact then there exists a function u such that

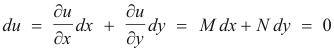
where

2)        M = ∂u/∂x ,      N = ∂u/∂y

Consequently, from 2) we get

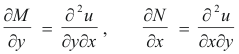
From calculus we know

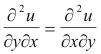
provided the partial derivatives are continuous. Thus ∂M/∂y = ∂N/∂x.

Part 2. We will now prove that if ∂M/∂y = ∂N/∂x, 1) will necessarily be exact i.e. that ∂M/∂y = ∂N/∂x is a sufficient condition for 1) to be exact. To do this it is sufficient to show that if ∂M/∂y = ∂N/∂x we can produce a function u(x, y) such that

3)        du = M dx + N dy

Let Φ(x, y) be a function for which

It is obtained by integrating M dx with respect to x, keeping y constant i.e.

(where S M ∂x denotes integration with respect to x, keeping y constant). Let us now take the partial of both sides of 4) with respect to y:

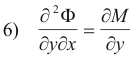
Now we know from calculus that

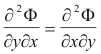
so 6) can be written

and because ∂M/∂y = ∂N/∂x 7) can be written as

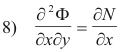
Let us integrate both sides of this last equation with respect to x, holding y fixed. The “arbitrary constant” will be any function of y. We will call it B'(y) for ease in referring to its primitive B(y). Integrating 8) with respect to x gives

9)        ∂Φ/∂y = N + B'(y)

We will now draw a function out of a magic hat and claim that it will meet the condition of 3) above. It is the function

10)      u = Φ(x, y) - B(y)

From 10) we get

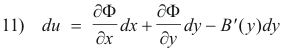
Substituting 9) into11) we get

            du = M dx + [N + B'(y) ] dy - B'(y) dy

or

            du = M dx + N dy 

References.

1. Earl D. Rainville. Elementary Differential Equations.