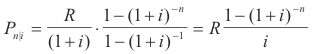Website owner:  James Miller

Derive the formula for the present value of an annuity in which the periodic payment is R dollars

Derivation. The desired present value is equal to the sum of the present values of the various payments. Using the formula for present value, P = A(1 + i)^-1 , we see that the present value of the payment due at the end of the first period is R(1 + i)^-1 , the present value of the payment due at the end of the second period is R(1 + i)^-2,etc. The present value of the last payment, due after n periods, is R(1 + i)^-n . Thus

            P_n|I = R(1 + i)^-1 + R(1 + i)^-2 + .... + R(1 + i)^-n

or

1)        P_n|I = R [(1 + i)^-1 + (1 + i)^-2 + .... + (1 + i)^-n ]

The terms in the right factor form a geometric progression in which (1 + i)^-1 is both the first term and common ratio. Using the formula for the sum of the first n terms of a geometric progression, 1) becomes