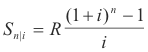Website owner:  James Miller

Derive the formula for the amount of an annuity

Derivation. Assume R dollars is invested at the end of each payment period. As soon as it is made, each payment is invested at compound interest at the rate of i per period, and is left until the end of the term. At the end of the term the last payment of R will have just been made and will amount to R. The next to the last payment will have been at interest for one period , and will amount to R(1 + i). The payment before that one will have been at interest for two periods and will amount to R(1 + i)² ,etc. The first payment will have been at interest for (n - 1) periods and will amount to R(1 + i)^n-1. The sum of these amounts is then

            S = R + R(1 + i) + R(1 + i)² + .... + R(1 + i)^n-1

The terms in the right member form a geometric progression in which the first term is R, the ratio is 1 + i, and the number of terms is n. Using the formula for the sum of the first n terms of a geometric progression we have