Methods of solving equations in one or more unknowns. Conditional equation. Solution set. Function. Linear systems. Quadratic equations.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Def. Equation. A statement of equality between two expressions. Equations are of two types: conditional equations and identities.

Def. Conditional equation. An equation which is true for only certain values of the variables. Conditional equations are usually simply called equations. A conditional equation is a type of open sentence. See open sentence.

Examples.

1) x + 3 = 5 is a true statement only when x = 2

2) x + y = 4 is a true statement for many pairs of values of x and y (such as x = 0, y = 4) but not true for many others

Def. Identity. An equation which is true for all values of the variables, with the exception of values of the variables for which the members of the equation have no meaning. In identities the sign is often used instead of the = sign.

Examples.

1) (x + y)²= x² + 2xy + y² is a true statement for all values of x and y

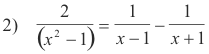
is true for all values of x except x = 1 and x = -1, values for which the left and right members of the equation have no meaning since it involves division by 0.

Def. Solution of a conditional equation. Any value of the variables which make both members equal. A solution is said to satisfy the equation. If only one variable is involved a solution is also called a root. To solve an equation means to find all the solutions or roots.

Examples.

1) x = 3 is a solution or root of the equation 2x + 4 = 10 since if we substitute x = 3 into the equation we obtain 2(3) + 4 = 10 and both members are equal. Thus we say x = 3 satisfies the equation.

2) The equation 3x + y = 6 is satisfied by many (x, y) pairs including (0, 6), (2, 0), and (1, 3)

Def. Solution set. The set of all solutions of a given equation, system of equations, inequality, etc. i.e. the set of all values for which the equation, system of equations, etc. is true.

Syn. truth set

Example 1. The solution set of the equation x² - 2x = 0 is the set consisting of the numbers 0 and 2.

Example 2. The solution set of the equation 3x + y = 6 is the set of all points lying on a particular straight line in the plane.

Def. Equivalent equations. Equations which have exactly the same solutions, or equivalently, equations that have the same solutions sets.

Example 1. The equations x - 4 = 0 and 2x = 8 are equivalent because both have the same solution , x = 4, and no other solutions.

Example 2. The equations x² = 1 and x⁴ = 2x² - 1 are equivalent because the solutions of both consist of the same numbers, -1 and +1, and no others.

Axiom 1. If the same quantity is added to, or subtracted from, both members of an equation, the result is an equation equivalent to the original one.

Example 1. Subtracting 3 from both members of the equation x + 3 = 0 gives the equivalent equation x = -3.

One of the most used operations of algebra is the operation of transposition.

Def. Transposition of a term. The operation of moving a term from one member of an equation to the other and changing its sign. This operation is equivalent to subtracting the term from both members of the equation. The equation x + 3 = 0 yields x = -3 after transposing the 3.

The operation of transposing a term in an equation yields an equivalent equation. The following example shows how transposition of terms is used to solve equations.

Problem. Solve the equation 3x - 5 = 2x + 6

Solution.

3x - 5 = 2x + 6

Transposing the -5 we get

3x = 2x + 6 + 5

Transposing the 2x we get

3x - 2x = 6 + 5

x = 11

Operations used in algebra in transforming equations. The following operations are used in algebra in transforming equations in the process of attempting to solve them. It should be noted that not all of these operations yield equations that are equivalent to the original. Some operations may yield equations with more solutions than the original, the extra solutions being called extraneous solutions. Other operations may yield equations with fewer solutions than the original equation.

1) Adding the same quantity to both sides of an equation.

2) Subtracting the same quantity from both sides of an equation.

3) Transposition of terms.

4) Multiplying both sides of an equation by the same quantity.

5) Dividing both sides of an equation by the same quantity.

6) Raising both sides of an equation to some power.

Example.

7) Taking some root of both sides of an equation.

Example.

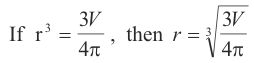
8) Taking reciprocals of both sides of an equation.

Example.

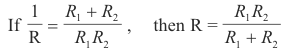
Operations 1), 2) and 3) always yield equivalent equations.

Operation 4) will yield an equivalent equation if both sides are being multiplied by a number. If, however, we multiply both sides of an equation by an expression that contains variables, we may introduce extraneous solutions. A derived equation that possesses extra solutions not satisfied by the original equation is said to be redundant with respect to the original equation.

Operation 5) will yield an equivalent equation if both sides are being divided by a number. If, however, we divide both sides of an equation by an expression that contains variables, the resulting equation may contain fewer solutions than the original. A derived equation that possesses fewer solutions than the original equation is said to be defective with respect to the original equation.

Operation 6) may introduce extraneous solutions.

Operation 7) may result in an equation with fewer solutions than the original.

If, in solving an equation, we use operations 4) or 6), it is important to check the solutions obtained by substituting them into the original equation, rejecting any that don’t satisfy it.

Def. Rational integral equation. A statement of equality between two rational integral expressions i.e. two polynomials. The degree of a rational integral equation is the degree of the term of highest degree present in the equation. An equation is called linear if it is of degree 1, quadratic if it is of degree 2, cubic if it is of degree 3, quartic if it is of degree 4 and quintic if it is of degree 5.

Examples.

3x²yz³ + xyz² = 4xy + 5 is an equation of degree 6.

3x + 2y = 3z + 1 is a linear equation in x, y, and z

5x² + xy = z + 1 a quadratic equation in x, y and z

x³ - 2x² = 4x + 2 is a cubic equation in x

I Solving equations in one unknown. The variables in an equation are often called unknowns. In trying to solve an equation we are looking for those values of the unknowns that will satisfy the equation. Solving an equation consists of a step-by-step process in which we attempt to manipulate the equation into a form that will give us a solution. In general, the process involves utilizing the various rules for manipulating algebraic expressions and algebraic equations. It is partially a trial and error process and there is no guarantee of success. The equation may be unsolvable by algebraic methods and one may be forced to use graphical methods to obtain the solution. In general, the more complicated an equation is, the more difficult it is to solve. Formulas do exist for the solutions of certain important kinds of equations, such as a quadratic, cubic and quartic equations in a single unknown. One important method of finding the roots of an equation in a single unknown is by a technique employing factoring.

Solution of equations in one unknown by factoring. This technique involves moving all terms of the equation to the left side of the equation (leaving a 0 on the right side), simplifying the expression on the left side as much as possible, and then factoring the left side into a product in which at least one factor is of the form (ax + b). If one can manipulate the given equation into the form

1] (ax + b)( .......) = 0

a solution to the equation is given by that value of x that make the factor (ax + b) equal to zero i.e. it is given by the solution of the equation

2] ax + b = 0

which is x = -b/a .

Example. Solve x² - 7x + 10 = 0

Solution.

1] x² - 7x + 10 = 0

2] (x - 2)(x - 5) = 0

A value of x that makes either factor of 2] equal to zero is a root of 2] and also of 1]. We set the factors (x - 2) and (x - 5) equal to zero and obtain

x - 2 = 0

x = 2

x - 5 = 0

x = 5

We thus obtain as solutions x = 2 or 5.

Check. When x = 2, 1] becomes 2² - 7∙2 + 10 = 0

When x = 5, 1] becomes 5² -7∙5 + 10 = 0

We now note that one should never divide both members of an equation by an expression containing an unknown, because if this is done, one or more roots will be lost.

Thus in x² = 4x one must not divide by x. Doing this would give the single solution x = 4. The correct procedure is:

x² = 4x

x² - 4x = 0

x(x - 4) = 0

Setting both factors equal to zero, we get

x = 0

x - 4 = 0

x = 4

Thus x = 0 or 4.

Similarly, in

x² - 4 = x - 2

(x + 2)(x - 2) = x - 2

one must not divide by x - 2 since this would give only the one solution x = - 2. The correct way is

x² - 4 = x - 2

x² - x - 2 = 0

(x + 2)(x - 2) = 0

Setting both factors equal to zero, we get

x + 2 = 0

x = -2

x - 2 = 0

x = 2

Thus x = -2 or 2

Quadratic equations in one unknown. The general form of a quadratic equation in one unknown is

ax² + bx + c = 0

where a, b and c represent numbers. Thus the equation 3x² + 5x - 2 = 0 is a quadratic equation. All quadratic equations in one unknown can be solved by a method known as “completing the square”.

Solution of quadratic equations by completing the square. We illustrate the method by a couple of examples.

Problem 1. Solve x² + 6x - 7 = 0

Solution.

1) x² + 6x - 7 = 0

2) x² + 6x = 7

We now wish to make the left member of 2) a perfect trinomial square of the form

3) a² + 2ab + b² = (a + b)².

We ask ourselves what number we can add to both sides of 2) to do this. Here x corresponds to the a of 3) and we ask ourselves what number b needs to be. The answer is half the coefficient of x or 3. We need to add b² or 3² = 9 to both sides of the equation. We get

x² + 6x + 9 = 7 + 9

(x + 3)² = 16

Taking the square root of both sides we get

x + 3 = 4

Thus there are two solutions:

x = -3 + 4 = 1

and

x = -3 - 4 = -7

Check. Substituting 1 for x in 1) we get 1 + 6 -7 = 0.

Substituting -7 for x in 1) we get 49 - 42 + 7 = 0.

Problem 2. Solve 3x² + 12 x - 15 = 0

Solution.

1) 3x² + 12 x - 15 = 0

Step 1. Transpose the terms so that the terms containing x are on the left side and the others on the right side.

2) 3x² + 12 x = 15

Step 2. Divide both sides by the coefficient of x².

3) x² + 4x = 5

Step 3. Ask what number will make the left side a perfect square. The answer is the square of half the coefficient of x, or 2² = 4. Add that to both sides.

4) x² + 4x + 4 = 5 + 4

(x + 2)² = 9

Taking the square root of both sides we get

x + 2 = 3

Thus there are two roots

x = -2 + 3 = 1

and

x = -2 - 3 = -5

Check. x = 1: 3∙1² + 12∙1 - 15 = 0

x = -5: 3(-5)² + 12(-5) -15 = 75 - 60 - 15 = 0

Solution by Quadratic Formula. The general quadratic equation ax² + bx + c = 0 can be solved by the method of completing the square to create a general formula for the solution of any quadratic equation. The solution of any quadratic equation ax² + bx + c = 0 is given by the formula

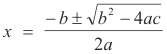
which is known as the Quadratic Formula.

Derivation

Example. Solve 3x² + 12 x - 15 = 0 by the Quadratic Formula.

Solution. Here a = 3, b = 12 and c = -15. Substituting these values into the Quadratic Formula gives

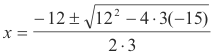
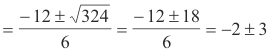
Thus x = 1, -5

Discriminant of a quadratic equation. The discriminant of the quadratic equation ax² + bx + c = 0 is the quantity b² - 4ac. The value of the discriminant provides information on the character of the roots as follows:

Let a, b, c be rational numbers. Then the roots are

real and unequal if and only if b² - 4ac > 0

real and equal if and only if b² - 4ac = 0

rational if and only if b² - 4ac is the square of a rational number

imaginary and unequal if and only if b² - 4ac < 0

Sum and product of the roots of a quadratic equation. The sum S and product P of the roots of the quadratic equation ax² + bx + c = 0 are given by

It then follows that a quadratic equation ax² + bx + c = 0 whose roots are x₁ and x₂ is given by x² -Sx + P = 0 where S = x₁ + x₂ and P = x₁∙x₂.

Example. A quadratic equation whose roots are x = 3 and x = 5 is x² - (3 + 5) x + 3∙5 = 0 or x² -8x + 15 = 0.

The concept of a function.

Def. Variable. A symbol which can assume any one of a set of values during a discussion.

Def. Constant. A symbol which can assume only one particular value during a discussion.

Letters at the end of the alphabet, such as x, y, z, u, v, w, are usually used to represent variables and letters at the beginning of the alphabet, such as a, b, c, ..., are usually used for constants.

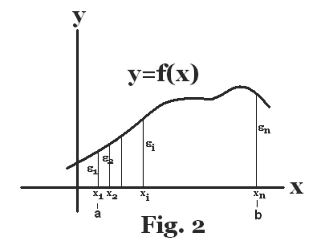
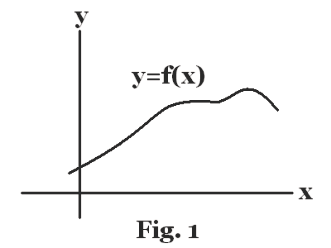
Def. Function. A variable y is said to be a function of a variable x, written y = f(x), if for each value that x can assume there is a corresponding value for y. The concept of a function y = f(x) is most easily understood by considering its graph in a Cartesian coordinate system. In Fig. 1 a variable y is depicted as a function of a variable x. The variable x is the independent variable and the variable y is the dependent variable. Now consider Fig. 2. As x progresses from point a to b on the x axis, passing through successive values x₁, x₂, x₃, ... , x_n, the values of y = f(x) progress through values ξ₁, ξ₂, ξ₃, ... ,ξ_n. The central idea is that as the independent variable x ranges over some range of values from some set, the dependent variable y varies, assuming a succession of values.

The variable to which values are assigned is called the independent variable. The other variable whose values are determined by the value of the independent variable is called the dependent variable. Saying that y is a function of x is equivalent to saying that y depends on x.

We now give a more formal definition:

A variable y is said to be a function of a second variable x if by some rule, device or means there is assigned to each of a certain set of values of x a single value for y.

Examples of functions.

1] The formula for the area of a circle, A = πr², gives the area A of a circle as a function of the radius r. To each value of r there corresponds a value for A.

2] The equation

y = 5x² + 3x + 2

is a function. It gives a value of y for each value of x in the interval consisting of the entire x axis.

● In general, any equation or formula that gives the value of one variable in terms of another represents a function.

3] A chart showing the air temperature at some point in space as measured over some period of time defines a function of temperature v.s. time for that location.

● We see from this last example that a function need not be defined by some formula or analytic expression. It can be defined by some chart, graph, or table.

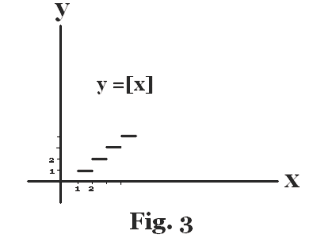
4] Let [x] represent the integral part of a real number i.e. the integer obtained by truncating the fractional part. For example, [2.1] = 2, [5.4] = 5 , etc. Then y = [x] is the function shown in Fig. 3.

Domain of definition of a function. In general, the independent variable is defined over some set of values. There are frequently restrictions, either implied or stated, on the values that may be assumed by the independent variable. The set of values over which the independent variable is defined is called the domain of definition of the function.

Example. In the case of the formula for the area of a circle, A = πr², the range of definition for the independent variable r is the positive numbers. A negative value of r makes no sense.

Functional notation. Symbols such as f, F, g, G, Φ, etc., are used to denote a function, the function values corresponding to x being denoted by f(x), F(x), g(x), G(x), Φ(x), etc. and read as "f of x" or "the f function of x," etc.

Graphical method for finding the roots of general equations in one unknown. The arsenal of methods for solving equations in one unknown by algebraic means is very limited. Some equations can be solved by factoring (probably mostly textbook type equations). Quadratic equations can be solved by the method of completing the square or by the quadratic formula. However, probably most of the equations that arise in practice in the real world are not solvable by algebraic means. What is needed is a method of finding the roots of any equation. That method is the graphical method. Suppose we are given an equation such as

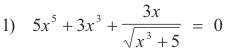
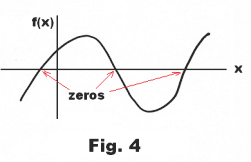
that we wish to solve (all terms are assumed to be on the left side and 0 on the right side). What we do is view the expression in the left member as a function of x and plot it. The roots of the equation correspond to the places where the graph of this function crosses the x axis (where it crosses the x axis is the situation where it has the value 0 and the equation is satisfied). Given some function f(x), the values of x at which the function crosses the x axis are called the zeros of f(x). See Fig. 4. Thus finding the solutions to an equation f(x) = 0 is tantamount to the problem of finding the zeros of the associated function f(x).

We can compute a root to any desired degree of accuracy by first determining the approximate position where it crosses the x axis and then narrowing down the location by using smaller and smaller increments. If we denote the expression in the left member of 1) by , 1) can then be written

and we plot versus x to find the zeros of , which represent the roots of the equation. This is the basis for what are called numerical methods for computing roots of equations.

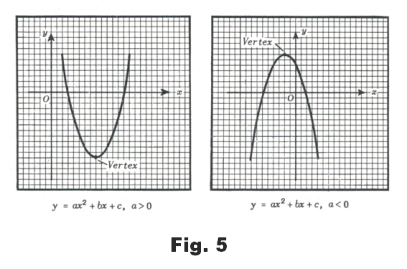
Graph of the quadratic function. The function

is called the quadratic function. The graph of any quadratic function is a parabola, facing either up or down. If a > 0, the parabola opens upward; if a < 0, the parabola opens downward. See Fig. 5. The places where the parabola crosses the x axis correspond to the roots of the quadratic equation

ax² + bx + c = 0.

II Solving equations in two or more unknowns.

Basic concepts of analytic geometry.

The basic idea of analytic geometry is that idea originated by Rene Descartes in the 1600's of representing an equation in two variables,

f(x, y) = 0,

graphically in a rectangular coordinate system. He introduced the ideas of a rectangular coordinate system and the coordinate representation of a point. Before his day there was no graphical means available for viewing an equation. People focused on solving equations in a single variable for the unknown, viewed everything totally algebraically, and an equation in two variables was viewed as indeterminate and uninteresting. An idea central to analytic geometry is that of a locus of an equation. The locus of an equation is the totality of all points whose coordinates satisfy the equation. The locus of an equation is the solution set of the equation, the solution set being the set of all solutions of the equation. We plot the solution set of an equation in a coordinate system to give ourselves a pictorial representation of the locus.

Def. Solution set. The set of all solutions of a given equation, system of equations, inequality, etc. E.g. the solution set of the equation x² - 2x = 0 is the set whose members are the numbers 0 and 2; the solution set of x² + y² = 4 is that set of coordinates (x, y) that satisfy the equation, corresponding in this case to a circle with center at the origin and radius 2; the solution set of the system, x + y = 1, x - y = 3, is the set whose only member is the ordered pair (2, -1); the solution set of the inequality 3x + 4y + z < 2 is the set of all ordered triplets (x, y, z) that represent points which are below the plane whose graph is 3x + 4y + z = 2 .

James and James. Mathematics Dictionary.

Def. Locus. Any system of points, lines, or curves which satisfies one or more given conditions. If a set of points consists of those points (and only those points) whose coordinates satisfy a given equation, then the set of points is the locus of the equation and the equation is the equation of the locus. E.g. the locus of the equation 2x + 3y = 6 is a straight line, the line which contains the points (0, 2) and (3, 0). The locus of points which satisfy a given condition is the set which contains all the points which satisfy the condition and none which do not; e.g. the locus of points equidistant from two parallel lines is a line parallel to the two lines and midway between them; the locus of points at a given distance r from a given point P is the circle of radius r with center art P.

James and James. Mathematics Dictionary.

Two fundamental problems of analytic geometry. Two fundamental problems of analytic geometry are:

1] Given an equation, to find the locus.

2] Given a locus defined by some geometrical condition, to find the corresponding equation. [For example, a problem such as: Find the equation of the locus of a point which is equidistant from the points (-2, 3) and (5, 8)].

Plane analytic geometry. In plane analytic geometry we deal with equations in two variables. Equations in two variables can be classified as:

1] Equations of the first degree in two variables, the general form of which is

ax + by + c = 0

2] Equations of the second degree in two variables, the general form of which is

ax² + bxy + cy² + dx + ey + d = 0

3] Equations of degree higher than two in two variables.

Any equation in two variables can be represented as a graph in a rectangular x-y coordinate system.

Fundamental theorems:

Theorem 1. The locus of an equation of the first degree in two variables is a straight line.

Theorem 2. The locus of an equation of the second degree in two variables is a conic (i.e. an ellipse, hyperbola, or parabola).

Note. Conics include some degenerate cases: 1) a point, 2) a straight line and 3) a pair of straight lines.

Linear systems. Consider the following problem.

Problem. The difference between two numbers in 9, and their sum is 13. What are the numbers?

Solution. Let

x = one number

and y = the other number

Then

1) x + y = 13

2) x - y = 9

The above problem has thus given rise to a system of two equations in two unknowns. To solve this system let us rewrite 1) as:

3) y = 13 - x

Now let us substitute 3) into 2) giving

4) x - (13 - x) = 9

5) 2x = 22

6) x = 11

Substituting 6) into 1) gives

7) y = 2

Many algebraic problems are most conveniently solved utilizing more than one unknown and more than one equation. We are thus led to the problem of solving systems of linear equations in more than one unknown. We call the equations of such systems simultaneous equations because we seek values for the unknowns that satisfy all the equations of the system simultaneously.

Methods of solving linear systems. There are two methods for solving linear systems. We will illustrate them for the case of two equations in two unknowns. Both are based on eliminating one of the unknowns.

Method of substitution. Find the value of one unknown in either of the given equations and substitute this value in the other equation.

Example. Solve the system

1) 3x + y = 6

2) 7x + 5y = -2

Solving 1) for y we get

3) y = 6 - 3x

Substituting 3) into 2) gives

4) 7x + 5(6 - 3x) = -2

5) -8x = -32

6) x = 4

Substituting 6) into 3) yields

7) y = -6

Method of addition or subtraction. 1. Multiply the equations by such numbers as will make the coefficients of one of the unknowns numerically equal. 2. If the signs of the numerically equal coefficients are unlike, add the resulting equations; if like, then subtract them.

Example. Solve the system

1) 3x + y = 6

2) 7x + 5y = -2

Multiplying 1) by 5 gives

3) 15x + 5y = 30

Now subtract 2) from 3)

4) 8x = 32

5) x = 4

Substituting 5) into 1) gives

6) y = -6

Not all linear systems have solutions. Under what circumstances may they not have solutions? An intuitive understanding of this question can be obtained by examining the graphs shown in Fig. 6.

1. Fig. 6a. In Fig. 6a the linear system consists of two lines, l₁ and l₂,which cross. This is the usual situation and the system has a single solution consisting of the point of intersection.

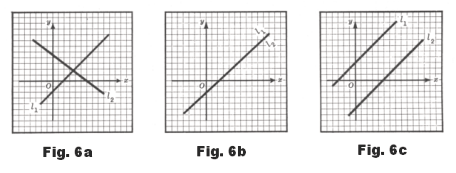
2. Fig. 6b. In Fig. 6b the linear system consists of two coincident lines, l₁ and l₂. Here the system has an unlimited number of solutions consisting of all points on the line. An example of such a system is

1) x - y = 2

2) 6x - 6y = 12

where we note that 2) can be obtained from 1) by multiplying 1) by 6. In general, if one equation is a multiple of another, the two equations represent the same line.

2. Fig. 6c. In Fig. 6c the linear system consists of two parallel lines, l₁ and l₂. This system has no solutions. The equations are said to be inconsistent. An example of such a system is

1) x - y = 5

2) x - y = -3

where we note that these equations state a contradiction since 3x + 5y cannot equal both 5 and -3.

Solving a system of three equations in three unknowns. To solve a system of three equations in three unknowns eliminate one unknown from any two of the equations and then eliminate the same unknown from any other pair of equations.

Example. Solve the system

1) 2x - y + z = 3

2) x + 3y - 2z = 11

3) 3x - 2y + 4z = 1

To eliminate z between 1) and 2) multiply 1) by 2 and add to 2) to get

4) 5x + y = 17

To eliminate z between 2) and 3) multiply 2) by 2 and add to 3) to obtain

5) 5x + 4y = 23

Solving 4) and 5) simultaneously we get

6) 3y = 6

7) y = 2

Substituting into 5) we get

8) x = 3

Substituting x = 3, y = 2, into 1) we obtain

9) z = -1

Quadratic equations in two variables. The general quadratic equation in two variables has the form

ax² + 2bxy + cy² + 2dx + 2ey + f = 0

It is either a conic or limiting form of a conic. The type of conic can be determined from the value of the invariant quantity b² - ac as follows:

b² - 4ac < 0	ellipse or limiting form (i.e. circle, point, imaginary locus)
b² - 4ac = 0	parabola
b² - 4ac > 0	hyperbola or limiting form (i.e. intersecting lines)

References

Hawks, Luby, Touton. First-Year Algebra

Hawks, Luby, Touton. Second-Year Algebra

Murray R. Spiegel. College Algebra (Schaum)

Raymond W. Brink. A First Year of College Mathematics

Frank Ayres. First Year College Mathematics (Schaum)

James / James. Mathematics Dictionary