Complex variable methods applied to fluid flow, electrostatics, heat flow. Potential functions. Conservative, irrotational and solenoidal fields. Equipotential lines, streamlines, isothermal lines and flux lines.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Some definitions

Def. Potential function relative to a given vector-valued function F. A scalar-valued function Φ such that grad Φ = F, or - grad Φ = F, depending on the convention used. If F is velocity, then Φ is the velocity potential.

For more information on potential functions see Work, conservative force fields, scalar potential

Def. Potential flow. Alternatively called irrotational flow, flow in which the velocity v is given by v = grad Φ. A necessary and sufficient condition for this to be so is that curl v = 0, i.e. the vorticity is everywhere zero.

International Dictionary of Applied Mathematics

Def. Velocity potential function of an irrotational fluid. The velocity potential function Φ(x, y, z) of an irrotational fluid is a scalar point function whose directional derivative in any direction represents the component of the velocity of flow in that direction, and the gradient

is the velocity vector v.

Hauser. Complex Variables. p. 350

Spiegel. Complex Variables. p. 234

Def. Stationary or steady flow. The velocity of the fluid may vary from point to point but at any point P it remains constant i.e. the velocity depends only on the position and not on time.

Def. Streamline. In steady flow, the paths of the fluid particles.

Def. Two dimensional fluid flow. In fluid flow, the situation where there exists a particular plane such that the fluid motion in that plane is identical to that in all planes parallel to it, enabling one to treat the problem as a two dimensional fluid flow problem.

Equation of continuity for an incompressible fluid. The equation of continuity for an incompressible fluid is

where V_x, V_y and V_z represent the x, y and z components of the velocity V of the fluid at point P(x, y, z). This equation expresses the condition that the quantity of fluid contained within an infinitesimal volume element is constant, that there are no sources or sinks within the element where fluid appears or disappears.

*****************************************************

Vectors and vector fields in two-dimensional space

Complex representation of a two-dimensional vector. The complex representation of a vector A = (a₁, a₂) = a₁i +b₂j in the xy plane is A = a₁ + a₂i in the z plane.

Unit tangent and unit normal vectors at a point on a curve. Let a curve C in the xy plane be defined by

1) r(s) = x(s)i + y(s)j

where s represents distance along the curve measured from some specified point s = 0 on the curve. The unit tangent vector t at point P on C is a unit vector tangent to the curve at P pointed in the direction of increasing s and given by

2) t = dr/ds = [dx(s)/ds] i + [dy(s)/ds] j

The unit normal vector n at point P on C, a unit vector perpendicular to t and rotated + π/2 from the positive direction of t, is given by

3) n = [-dy(s)/ds] i + [dx(s)/ds] j

Proof

Tangential and normal components of a vector point function evaluated along a curve. Let F = [F_x(x, y), F_y(x, y)] be a vector point function defined over some region R of the z plane and let C be a curve within R. Let F_t = F_t(x, y) and F_n = F_n(x, y) be the tangential and normal components of F in the directions t and n at z = x + iy on C. F_t , consisting of the projection of F in the direction t, is given by F_t = F•t i.e. by

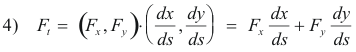
F_n , consisting of the projection of F in the direction n, is given by F_n = F•n i.e. by

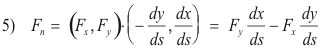
Conservative field. A vector field F = [F_x(x, y), F_y(x, y)] defined over some region R is said to be conservative or irrotational if the integral of F_t = F•t around every closed curve C in R vanishes i.e.

where s is arc length along C from some specified start point s = 0. The integral

is called the circulation of the flux F along C. A vector field F is conservative if and only if Curl F = 0 everywhere in R.

Solenoidal field. A vector field F = [F_x(x, y), F_y(x, y)] defined over some region R is said to be solenoidal if the integral of F_n = F•n around every closed curve C in R vanishes i.e.

where s is arc length along C from some specified start point s = 0. A vector field F is solenoidal if and only if div F = 0 everywhere in R.

*****************************************************

I Fluid flow

Complex variable methods for solving fluid flow problems

The solution of many important problems in fluid flow can be obtained by complex variable methods under the following conditions:

1. The flow is two dimensional.

2. The flow is stationary or steady.

3. The flow is irrotational. A necessary and sufficient condition for the flow to be irrotational is that the curl of the velocity be everywhere zero. If this condition is met there will exist a potential function Φ, called the velocity potential function, such that V = grad Φ where V is the fluid velocity at any point P i.e. there will exist a function Φ such that

where V_x and V_y are the x and y components of V. Thus under irrotational flow

4. The fluid is incompressible. If a fluid is incompressible the following equation of continuity for an incompressible fluid is satisfied:

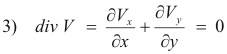
5. The fluid is non-viscous. A moving viscous fluid tends to adhere to the surface of objects in its path. In a fluid without viscosity, without internal friction, the pressure forces on a surface are perpendicular to the surface. In a fluid with viscosity this isn’t true. A fluid which is non-viscous and incompressible is often called an ideal fluid. Ideal fluids, of course, don’t exist but some fluids may approach them.

The complex potential function. If we substitute 2) above into 3) we get

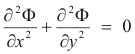
Thus we see that if the fluid is incompressible and the flow is irrotational the velocity potential Φ satisfies Laplace’s equation and is thus harmonic. It then follows that there must exist a conjugate harmonic function, say Ψ(x, y), such that

4) Ω(z) = Φ(x, y) + iΨ(x, y)

is analytic. The function Ω(z) is called the complex potential function. The function Ψ(z) is called the stream function.

Now dΩ/dz is given by

By the Cauchy-Riemann equations ∂Ψ/∂x = - ∂Φ/∂y, so 5) becomes

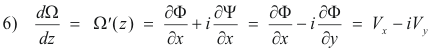
Thus the velocity (sometimes called the complex velocity) is given by the conjugate of Ω'(z)

and has the magnitude

Points at which the velocity is zero, i.e. Ω'(z) = 0, are called stagnation points.

The complex potential function Ω(z) is of fundamental importance in characterizing fluid flow.

Equipotential lines and streamlines. The one parameter families of curves

Φ(x, y) = α, Ψ(x, y) = β

where α and β are constants, are orthogonal families called respectively the equipotential lines and streamlines of the flow (the terms equipotential curves and stream curves are are also used).In steady flow the streamlines represent the actual paths of the fluid particles.

Complex potential functions associated with some simple fluid flows

1. Uniform flow. The complex potential function corresponding to the flow of a fluid at constant speed V₀ in a direction making an angle δ with the positive x axis is

Ω(z) = V₀ e^-iδ z

See Fig. 1.

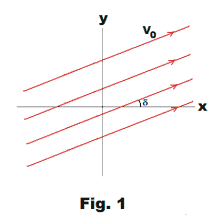
2. Source at z = a. The complex potential function corresponding to a fluid emerging at constant rate from a source at z = a is

Ω(z) = k ln(z - a)

where k > 0 is called the strength of the source. See Fig. 2.

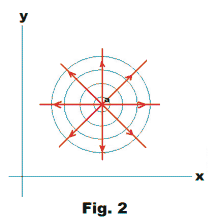
3. Sink at z = a. The complex potential function corresponding to a fluid disappearing at constant rate from a source at z = a is

Ω(z) = - k ln(z - a)

where k > 0 is called the strength of the source. See Fig. 3.

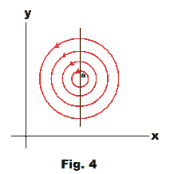
4. Flow with circulation. The flow corresponding to the complex potential function

Ω(z) = - ik ln(z - a)

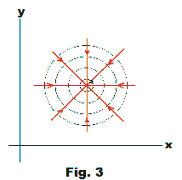
is shown in Fig. 4. The magnitude of the velocity of the fluid at any point is inversely proportional to the distance from a. The point z = a is called a vortex and k is its strength. The circulation

about any simple closed curve C enclosing z = a is equal in magnitude to 2πk. By changing k to -k the complex potential function corresponding to a clockwise vortex is obtained.

II Electrostatics

Electric field created by an electric charge. Coulomb’s law states that the force F which acts on a point charge q from the presence of another point charge Q is given by

where r is the distance between q and Q and κ is a proportionality constant that depends on the medium in which the charges reside. The force is one of repulsion or attraction depending on whether the charges are of the same or opposite charge. A distribution of charge in space, be it continuous, discrete, or some combination sets up an electric field. If a unit positive charge is placed at any point P not already occupied by charge, the force acting on this charge is called the electric field intensity at P. The electric field intensity E at a point P arising from an aggregate of charges can be computed directly from Coulomb’s law with the total intensity at the point being simply the sum of all the contributions from the individual charges in the aggregate. An electric field of this type, arising from an aggregate of stationary charges, is a conservative field. As a consequence there exists a potential function Φ, called the electrostatic potential, such that E = - grad Φ.

Two-dimensional electric fields. Let L be a line perpendicular to the xy plane at point (x₀, y₀) along which a charge of constant magnitude ρ per unit length is distributed. Such a distribution of charge is called a line charge of density ρ. The electric field from a line charge is two-dimensional i.e. the electric field is identical in all planes perpendicular to the line charge. Moreover, the electric field due to any number of parallel line charges is two-dimensional. The parallel elements of a cylindrical surface perpendicular to the xy plane can be thought of as line charges. Consequently, if S is a cylindrical surface whose elements are perpendicular to the xy plane and whose surface has a constant charge per unit area, it will create an electric field that is two-dimensional. Line charges illustrate two-dimensional charge distributions. Two-dimensional charge distributions give rise to two-dimensional electric fields.

Only electric fields that are two-dimensional are amenable to complex variable methods.

If the electric field is two-dimensional

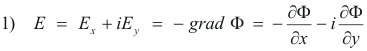
where E_x and E_y are the x and y components of E. Thus

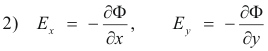
If E_t denotes the component of the electric field intensity tangential to any simple closed curve C

Gauss’ theorem. Let C be any simple closed curve in the xy plane having a net charge q in its interior (actually an infinite cylinder enclosing a net charge q) and E_n be the normal component of the electric field intensity. Then

If C does not enclose any net charge, this reduces to

Thus the field E is solenoidal and

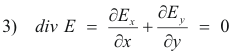
The complex electrostatic potential. Substituting 2) into 3) we get

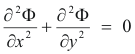
Thus Laplace’s equation is satisfied and Φ is harmonic at all points not occupied by charge. It then follows that there must exist a harmonic function Ψ(x, y) conjugate to Φ such that

4) Ω(z) = Φ(x, y) + iΨ(x, y)

is analytic in any region not occupied by charge. The function Ω(z) is called the complex electrostatic potential or, briefly, the complex potential.

Since

(from Cauchy-Riemann equations, ∂Ψ/∂x = - ∂Φ/∂y), we have

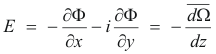
and the magnitude of E is given by

The families of curves

Φ(x, y) = α, Ψ (x, y) = β

are called equipotential lines and flux lines respectively

III Heat flow

Heat flow within an object. Let G be some solid object in which the temperature is not the same throughout but instead, for some reason or other, the temperature varies from point to point. Perhaps G might be a rock sitting in the sun and the warming of the sun is causing internal temperature differentials. If there are temperature variations within G then there will be heat flow from one point to another because heat flows by conduction from points of higher temperature to points of lower temperature. Heat will continue to flow until all points within G

are of the same temperature. At any particular point within an object the heat flow can be viewed in the same way as fluid flow. The flow rate is given by the amount of flux or heat passing through a square unit of cross-sectional area perpendicular to the direction of flow per unit of time.

Let the temperature within G at a particular time t = t₀ be given by the function T = T(x, y, z) defined over region G. See Fig. 5. The flow rate Q, called heat flux, at a particular point P:(x, y, z) within G, is given by

1) Q = -k grad T(x, y, z)

Q is a vector quantity pointed in the direction of heat flow with a magnitude giving flow rate in terms of the amount of heat passing through a square unit of cross-sectional area perpendicular to the direction of flow per unit of time. The constant k is called the thermal conductivity and depends on the material of which the solid is made. It specifies the heat energy per unit time per unit area which is caused to flow in the material due to a unit change in temperature per unit distance. The minus sign is included because the flow of heat energy is in the direction of decreasing temperature. The function T(x, y, z) constitutes a scalar point function defined over a simply connected region of space. Equation 1) shows Q to be the gradient of a scalar point function and as a consequence curl Q = 0. Thus Q represents a conservative (irrotational) field.

We have been considering heat flow in three dimensions. Let us now consider two-dimensional heat flow as one might find in a plate in which there were temperature differentials. The use of complex variable methods is limited to two-dimensional problems in which the temperature is steady i.e. it doesn’t change with time. In two dimensions T = T(x, y) and

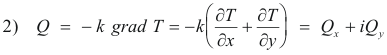
where Q_x and Q_y are the x and y components of Q. Thus

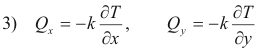
Let C be any simple closed curve in the xy plane. If Q_t and Q_n are the tangential and normal components of the heat flux and if steady state conditions prevail so there is no net accumulation of heat inside C, then

From 4) we conclude that the field Q is solenoidal and

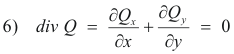
The complex temperature. Substituting 3) into 6) we get

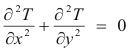
Thus Laplace’s equation is satisfied and T is harmonic. It then follows that there must exist a harmonic function Ψ(x, y) conjugate to T such that

4) Ω(z) = T(x, y) + iΨ(x, y)

is analytic. The function Ω(z) is called the complex temperature.

The families of curves

T(x, y) = α, Ψ (x, y) = β

are called isothermal lines and flux lines respectively.

Analogies between fluid flow, electrostatic and heat flow problems. The analogies between fluid flow, electrostatic and heat flow problems are obvious and methods employed in one field can be employed in the others. We can see that the role played by the fluid velocity in fluid flow problems corresponds to that played by the electric field intensity in electrostatic problems and heat flux in heat flow problems.

References

Spiegel. Complex Variables. (Schaum)

Hauser. Complex Variables with Physical Applications

James/ James. Mathematics Dictionary

International Dictionary of Applied Mathematics. (D. Van Nostrand)