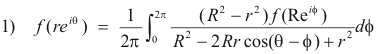
A full statement of Poisson’s integral formulas for a circle is as follows:

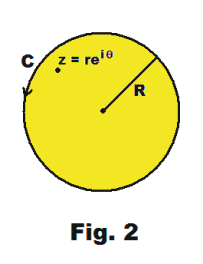
Theorem. Let f(z) be analytic inside and on the circle C defined by |z| = R, and let z = re^iθ be any point inside C. See Fig. 2 below. Then

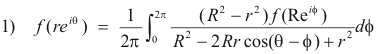
If u(r, θ) and v u(r, θ) are the real and imaginary parts of f(re^iθ) while u(R, θ) and v(R, θ) are the real and imaginary parts of f(Re^iθ), then

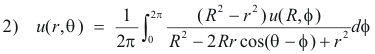
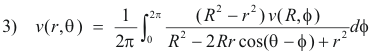
Proof. The proof utilizes the following concept:

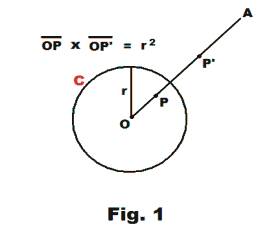
Def. Inverse of a point with respect to a circle. Let C be a circle with center at O and let P be any point inside or outside C. See Fig. 1. Draw line OA through point P. Then the inverse of point P is the point P' located on line OA whose distance from O is such that

Either of the points P and P' is called the inverse of the other and the center of the circle is called the center of inversion.   

Since z = re^iθ is any point inside C, we have by Cauchy’s integral formula

The inverse of the point P with respect to C lies outside C and is given by R²/ . Thus by Cauchy’s theorem,

We now subtract 5) from 4) to obtain

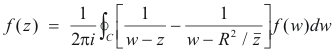
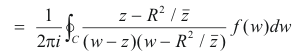
Now let z = re^iθ and w = Re^iθ. Then since = re^-iθ, we have

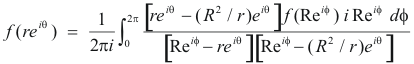
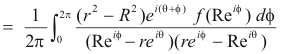
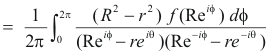
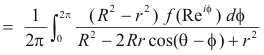
which is 1) above.

Since f(re^iθ) = u(r,θ) + i v(r,θ) and f(R ) = u(R, ) + i v(R, ) we obtain from 1)

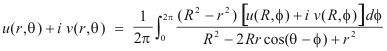
Thus we have 2) and 3) above

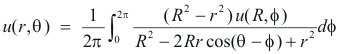
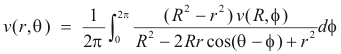
                                                            Source: Spiegel. Complex Variables (Schaum). p. 129-130