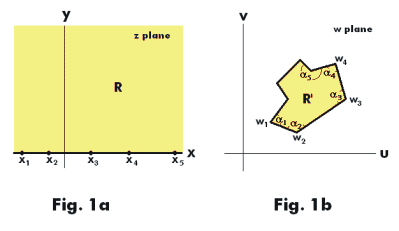
Prove. Consider a polygon in the w plane having vertices at w₁, w₂, ... , w_n with corresponding interior angles α₁, α₂, ... , α_n respectively. See Fig. 1b.

A transformation which maps the upper half plane R of the z plane onto the interior R' of the polygon and the real axis of the z plane onto the boundary of the polygon is given by

or

where the points x₁, x₂, ... , x_n on the real axis of the z plane are mapped respectively into the points w₁, w₂, ... , w_n of the polygon and A and B are complex constants.

Proof. The following will be more demonstration than proof. It will give intuitive insight into the transformation.

First observe that from 1] we obtain

3]        arg dw = arg dz + arg A + (α₁/π -1) arg(z - x₁) + (α₂/π -1) arg (z - x₂) + ... + (α_n/π -1) arg(z - x_n)

We direct our attention to what occurs as z moves along the real axis from the left, tracing out the polygon as it moves. As z passes each of the zeros at x₁, x₂, ... , x_n an event occurs. There is an abrupt change in argument at that point. And this abrupt change in argument causes an abrupt change arg dw which causes w to make an abrupt change in direction at that point i.e. it turns one of the corners of the polygon.

As z moves along the real axis from the left toward x₁, let us assume that w moves along a side of the polygon toward w₁. When z crosses from the left side of x₁ to the right side, θ₁ = arg(z - z₁) changes from π to 0 while all other terms in 3] stay constant. Fig. 2a shows the vector z - a₁ before z reaches point x₁. Fig. 2b shows the

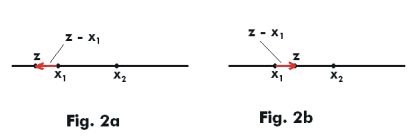
vector z - a₁ after z has passed x₁. We see that vector z - a₁ changes from a left pointing vector to a right pointing vector i.e. changes in direction from π to 0. Consequently arg dw decreases by

            (α₁/π -1) arg(z - x₁) = (α₁/π -1)π = α₁ - π

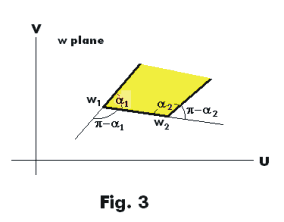
or, what is the same thing, increases by π - α₁ (an increase being in the counterclockwise direction). As a consequence of this when w reaches point w₁, it turns through the angle π - α₁ and then moves along the side w₁w₂ of the polygon. See Fig. 3.

When z moves through point x₂ the same thing happens. Arg (z - x₂) changes from π to 0 while all other terms in 3] stay constant. Thus another turn through an angle of π - α₂ at point w₂ is made. We thus see that as z moves along the x axis w traces out the polygon.