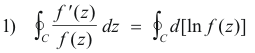
Prove: Argument principle. Let f(z) be analytic inside and on a simple closed curve C, except for a finite number of poles inside C. Let Z and P be the number of zeros and poles (multiplicities counted, each zero or pole counted a number of times equal to its order) inside C. Let Δ arg f(z) be the change in arg f(z) as z makes one trip about C in the positive (counterclockwise) direction. Then 

            Δ arg f(z) = 2π (Z - P)

Proof. We note that

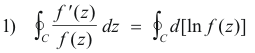
and

From the formula ln z = ln r + iθ we write

3)        ln f(z) = ln |f(z)| + i arg f(z)

Using 3) in 2) and remembering that ln |f(z)| is the same at the beginning and at the end of any closed curve we have

Thus, from 1) and 4),

Now

so

            Δ arg f(z) = 2π (Z - P)

References

  Mathematics, Its Content, Method and Meaning. Vol. I

  Wylie. Advanced Engineering Mathematics

  Hauser. Complex Variables with Physical Applications