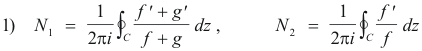
Prove. If f(z) and g(z) are analytic inside and on a simple closed curve C and if |g(z)| < |f(z)| on C, then f(z) + g(z) and f(z) have the same number of zeros inside C.

Proof. This theorem is a direct consequence of Theorem 3. Because f(z) and f(z) + g(z) have no poles and because f(z) and g(z) satisfy the conditions of Theorem 3, f(z) and f(z) + g(z) must have the same number of zeros inside C.

This theorem can also be proved by another method. Let F(z) = g(z)/f(z) so that g(z) = f(z)F(z), or briefly, g = fF. Let N₁ and N₂ be the number of zeros inside C of f + g and f respectively. Then

and

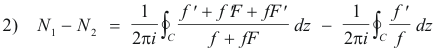
Finally,

We now observe that 1 + F cannot be zero since if F = -1, then | F | = 1 and | g | = | f | , which is contrary to the fact that | g | < | f | . Thus F'/(1+F) is analytic inside and on C and the integral in the right member of 3) is zero by Cauchy’s theorem. Thus N₁ = N₂.

References

  Spiegel. Complex Variables (Schaum)

  Hauser. Complex Variables with Physical Applications