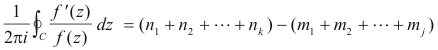Prove: Let f(z) be analytic inside and on a simple, closed curve C , except for j poles of orders m₁, m₂, ... m_j at points α₁, α₂, ..., α_j and k zeros of orders n₁, n₂, ... n_k at points β₁, β₂, ..., β_k, all located in the region inside C. Suppose that f(z) 0 on C. Then

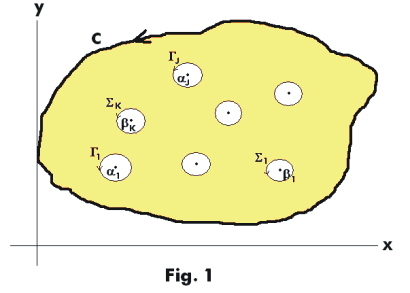
Proof. Enclose each of the poles by non-overlapping circles Γ₁, Γ₂, ... , Γ_j and each of the zeros by non-overlapping circles Σ₁, Σ₂, ... , Σ_{k ,} all contained within C, as shown in Fig. 1. Then

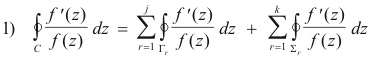
                    = (- 2πim₁ - 2πim₂ - ... -2πim_j ) + (2πin₁ + 2πin₂ + ... + 2πin_k)

                    = 2πi [(n₁ + n₂ + ... + n_k) - (m₁ + m₂ + ... + m_j)]

or