Prove: If f(z) has a pole of order m at z = a, then the residue of f(z) at z = a is given by

if m =1, and by

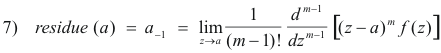
if m > 1.

Proof. We wish to prove that

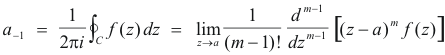
If f(z) has a pole of order m at z = a, then f(z) = g(z)/(z - a)^m where g(z) is analytic inside and on C, and g(a) 0. Thus

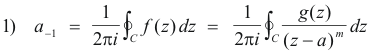
We shall now employ Cauchy’s integral formula

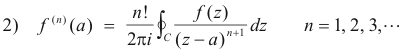
which we shall rewrite as

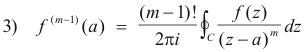
or, changing notation,

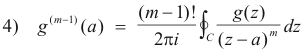
Thus 1) above becomes

Since

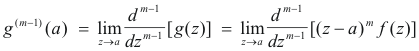
5) becomes

If we define 0! = 1, the above also proves the case for m = 1, which corresponds to the case of n = 0 in Cauchy’s integral formula 2).