Prove: Residue theorem. Let f(z) be analytic inside and on a simple closed curve C except at the singularities a, b, c, ... inside C which have residues given by a_r, b_r, c_r ... . Then

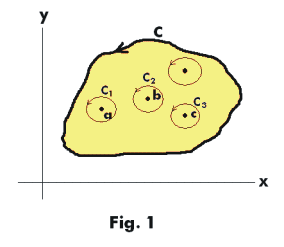
Proof. Construct circles C₁, C₂, C₃, ... centered at a, b, c, ... , of such radii as to lie entirely within C as shown in Fig. 1.

Now by Theorem 6 in the section on Complex integration and Cauchy’s theorem we have

Since

we have