Prove: Taylor’s theorem. Let f(z) be analytic inside a circle C centered at a and let z be a point inside C. Then

Proof. Let z be any point inside C. Construct a circle C₁ inside C with center at a and enclosing z. Let w be a point on C₁. See Fig. 1.

Our first step is to prove the following lemma. 

Lemma. For any three variables w, a and z the following identity holds:

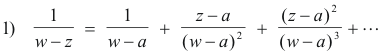
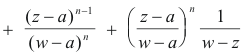
Proof. First we write

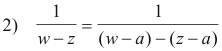
Now multiply both numerator and denominator of the right member by the fraction 1/(w - a) to get

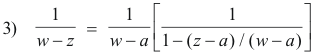
We now wish to employ the following identity:

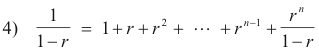
Where does this identity come from? It comes from the formula for the sum of a geometric progression

5)        a + ar + ar² + ... + ar^n-1 = a(1- rⁿ)/(1- r) ,

an identity valid for both real and complex numbers.

Letting a = 1 in 5) we get

6)        1 + r + r² + ... + r^n-1 = 1/(1 - r) - rⁿ/(1- r)

which, with a transposition, is 4).

Now let r = (z - a)/(w-a) and substitute into 4)

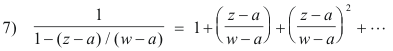
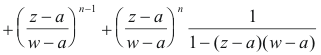
We now substitute 7) into 3) to obtain

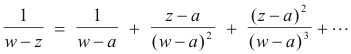
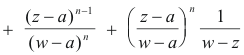
which is 1).

End of Proof.

Using the above lemma we will now proceed to prove our main theorem.

By Cauchy’s integral formula we have

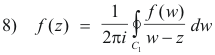
Substituting 1) into 8) we get

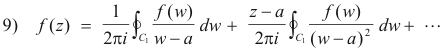
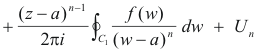
where

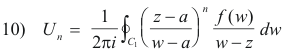
Using Cauchy’s integral formulas

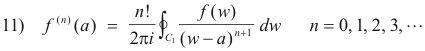
9) becomes

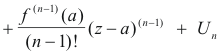
We now wish to show that . Doing so will conclude the proof. 

First note that

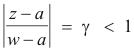
where is a constant. Second, note that on C₁, the function f(w) must acquire some finite maximum value i.e. it is bounded. Why? Because C₁ lies in an analytic region and so there can be no singular points on C₁ where the function might become infinite. Let M be the maximum of f(w) on C₁. The radius r₁ of C₁ is given by r₁ = |w - a|. We will also make use of the following observation:

            |w - z| = |(w - a) - (z - a)| r₁ - |z - a|

We now employ Property 5 of line integrals which states that

where |f(z)| M ( i.e. M is an upper bound of |f(z)| on C) and L is the length of C. The length of C₁ is 2πr₁ so

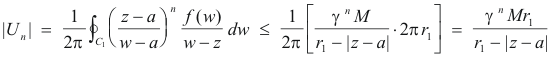
Because < 1 it can be seen that

since

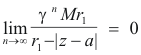
References

  Spiegel. Complex Variables (Schaum)

  Wylie. Advanced Engineering Mathematics