Prove: If in any analytic function w = u(x, y) + i v(x, y) the variables x and y are replaced by their equivalents in terms of z and , namely,

w will appear as a function of z alone.

Proof. Let us regard w, by virtue of the given substitutions, as formally a function of the new independent variables z and . To show that w depends only on z and does not involve , it is sufficient to compute and verify that it is identically zero. Now

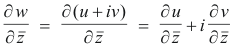
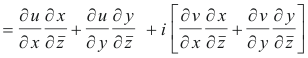
From 1) above we get

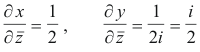
Thus

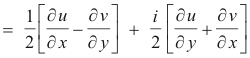
Because w is an analytic function, u and v satisfy the Cauchy-Riemann equations. Consequently each of the bracketed quantities in the last expression vanish and . Thus w is independent of .

                                                                                    Wylie. Advanced Engineering Mathematics. p. 549-550