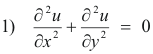
Prove. Let u(x, y) be harmonic in some region R. Then there exists a function v(x, y) such that f(z) = u(x, y) + iv(x, y) is analytic in R.

Proof. By the definition of a harmonic function u(x, y) satisfies Laplace’s equation. Thus

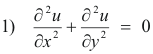
for all (x, y) in R. Rewriting 1) we get

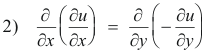
Now if for two functions M(x, y) and N(x, y) we know that

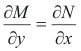
then M dx + N dy = 0 is an exact differential equation and there exists some function Φ such that dΦ = M dx + N dy. If in 2) we let M = -∂u/∂y and N = ∂u/∂x we see that 2) is an exact differential equation and there exists some function v(x, y) such that

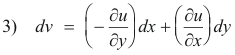
Taking the partial derivative of 3) with respect to x we get

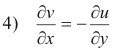
Taking the partial derivative of 4) with respect to y we get

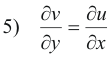
Thus from 4) and 5) we see that u and v satisfy the Cauchy-Riemann equations. Since u(x, y) satisfies Laplace’s equation, the second partial derivatives exist and, consequently, the first partial derivatives ∂u/∂x and ∂u/∂y are continuous in R. Thus the function f(z) = u(x, y) + iv(x, y) is analytic in R.